题目内容
6.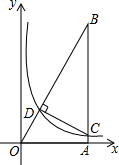 如图,Rt△AOB中,点A,B的坐标分别为(4,0),(4,8),C为AB上一点,双曲线y=$\frac{k}{x}$(k>0)经过点C,交OB于点D,且CD⊥OB.
如图,Rt△AOB中,点A,B的坐标分别为(4,0),(4,8),C为AB上一点,双曲线y=$\frac{k}{x}$(k>0)经过点C,交OB于点D,且CD⊥OB.(1)求双曲线的解析式;
(2)求四边形OACD的面积.
分析 (1)先求得直线OB的解析式,与y=$\frac{k}{x}$(k>0)联立方程得到D的坐标为($\sqrt{\frac{k}{2}}$,$\sqrt{2k}$),然后根据垂直的性质设直线CD的解析式为y=-$\frac{1}{2}$x+b,代入C(4,$\frac{k}{4}$),求得CD解析式,然后与直线OB的解析式联立方程得到D的坐标为D($\frac{k+8}{10}$,$\frac{k+8}{5}$),即可得出$\frac{k+8}{10}$=$\sqrt{\frac{k}{2}}$,解方程即可求得k的值.
(2)求得C的坐标,从而求得BC,根据勾股定理求得OB,然后根据相似三角形的性质列出$\frac{{S}_{△BDC}}{{S}_{△BAO}}$=($\frac{BC}{OB}$)2=$\frac{45}{64}$,根据△OAB的面积求得△BDC的面积,根据S四边形OACD=S△OAB-S△BDC即可求得.
解答 解:(1)∵B的坐标分别为(4,8),
∴直线OB的解析式为y=2x,
解$\left\{\begin{array}{l}{y=2x}\\{y=\frac{k}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\sqrt{\frac{k}{2}}}\\{y=\sqrt{2k}}\end{array}\right.$,
∴D($\sqrt{\frac{k}{2}}$,$\sqrt{2k}$),
∵点A,B的坐标分别为(4,0),(4,8),C为AB上一点,
∴AB⊥x轴,
∵双曲线y=$\frac{k}{x}$(k>0)经过点C,
∴C(4,$\frac{k}{4}$),
∵CD⊥OB,
设直线CD的解析式为y=-$\frac{1}{2}$x+b,
代入C(4,$\frac{k}{4}$)得,$\frac{k}{4}$=-2+b,
解得b=$\frac{k}{4}$+2,
∴直线CD的解析式为y=-$\frac{1}{2}$x+$\frac{k}{4}$+2,
解$\left\{\begin{array}{l}{y=2x}\\{y=-\frac{1}{2}x+\frac{k}{4}+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{k+8}{10}}\\{y=\frac{k+8}{5}}\end{array}\right.$,
∴D($\frac{k+8}{10}$,$\frac{k+8}{5}$),
∴$\frac{k+8}{10}$=$\sqrt{\frac{k}{2}}$,
解得k1=2,k2=32(舍去),
∴双曲线的解析式为y=$\frac{2}{x}$;
(2)把x=4代入y=$\frac{2}{x}$得,y=$\frac{1}{2}$,
∴C(4,$\frac{1}{2}$),
∴AC=$\frac{1}{2}$,
∴BC=8-$\frac{1}{2}$=$\frac{15}{2}$,
∵∠BDC=∠BAO=90°,∠DBC=∠ABO,
∴△BDC∽△BAO,
∴$\frac{{S}_{△BDC}}{{S}_{△BAO}}$=($\frac{BC}{OB}$)2
∵OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=$\sqrt{80}$,
∴$\frac{{S}_{△BDC}}{{S}_{△BAO}}$=($\frac{\frac{15}{2}}{\sqrt{80}}$)2=$\frac{45}{64}$,
∵S△OAB=$\frac{1}{2}$×4×8=16,
∴S△BDC=16×$\frac{45}{64}$=$\frac{90}{8}$,
∴S四边形OACD=S△OAB-S△BDC=16-$\frac{90}{8}$=$\frac{38}{8}$.
点评 本题考查了反比例函数系数k的几何意义,表示成C、D点的坐标是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )| A. | a和d | B. | a和c | C. | b和d | D. | b和c |
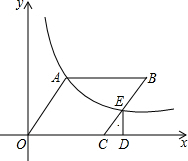 如图,在平面直角坐标系中,?OABC的顶点C的坐标为(3,0),∠AOC=45°,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A交BC于点E,过点E作ED⊥x轴于点D,ED=1.
如图,在平面直角坐标系中,?OABC的顶点C的坐标为(3,0),∠AOC=45°,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A交BC于点E,过点E作ED⊥x轴于点D,ED=1.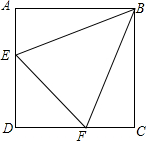 如图,点E,F分别在正方形ABCD的边AD,CD上,∠EBF=45°,连接EF,求证:EF=AE+CF.
如图,点E,F分别在正方形ABCD的边AD,CD上,∠EBF=45°,连接EF,求证:EF=AE+CF. 如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.
如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.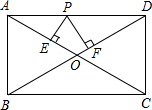 如图,在矩形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F.如果AB=5,AD=9.那么PE+PF的值.
如图,在矩形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F.如果AB=5,AD=9.那么PE+PF的值.