题目内容
18.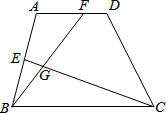 如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )
如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )| A. | 95 | B. | 100 | C. | 105 | D. | 110 |
分析 先由三角形的外角性质求出∠ABC=75°,再由梯形的性质得出∠A+∠ABC=180°,即可求出∠A的度数.
解答 解:∵∠AEG=∠ABC+∠GCB,
∴∠ABC=∠AEG-∠GCB=95°-20°=75°,
∵AD∥BC,
∴∠A+∠ABC=180°,
∴∠A=180°-75°=105°;
故选:C.
点评 本题考查了梯形的性质、平行线的性质、三角形的外角性质;熟练掌握梯形的性质,由三角形的外角性质求出∠ABC的度数是解决问题的关键.

练习册系列答案
相关题目
7.已知方程x-2y+3=8,则整式x-2y的值为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 15 |
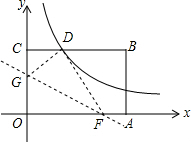 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
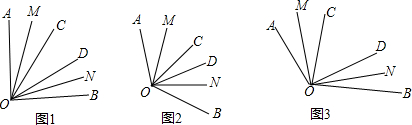
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.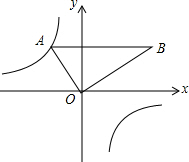 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.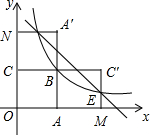 如图,四边形OABC是边长为2的正方形,函数y=$\frac{k}{x}(x>0)$的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=$\frac{k}{x}(x>0)$的图象交于点E、F,则直线EF与x轴的交点坐标为(5,0).
如图,四边形OABC是边长为2的正方形,函数y=$\frac{k}{x}(x>0)$的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=$\frac{k}{x}(x>0)$的图象交于点E、F,则直线EF与x轴的交点坐标为(5,0).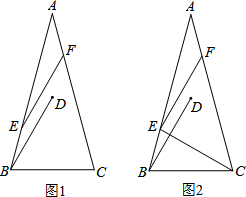 在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.