题目内容
8.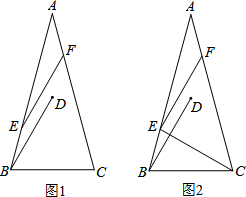 在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上. (1)如图1,直接写出∠ABD和∠CFE的度数;
(2)图1中:AE和CF有什么数量关系?请说明理由;
(3)如图2,连接CE,判断△CEF的形状并加说明理由.
分析 (1)由旋转可得到∠DBC=60°,再利用等腰三角形的性质可求得∠ABC,可求得∠ABD,利用平移可得到∠AEF=∠ABD,在△AEF中利用外角的性质可求得∠CFE;
(2)连接CD、DF,可证明四边形BDFE为平行四边形,可证得EF=BD=CD,再结合条件可求得∠A=∠CFD,∠AEF=∠ACD,可证明△AEF≌△FCD,可证明AE=CF;
(3)过点E作EG⊥CF于G,可证明G为CF的中点,从而可证得EF=EC,可得△CEF为等腰直角三角形.
解答 解:
(1)∵线段BC逆时针旋转旋转60°得到BD,
∴∠CBD=60°,
∵AB=AC,∠A=30°,
∴∠ABC=$\frac{180°-30°}{2}$=75°,
∴∠ABD=∠ABC-∠DBC=75°-60°=15°,
∵BD平移得到EF,
∴EF∥BD,
∴∠AEF=∠ABD=15°,
∵∠A=30°,
∴∠CFE=∠A+∠AEF=30°+15°=45°;
(2)AE=CF.
理由:如图1,连结CD、DF,
∵线段BC绕点B逆时针旋转60°得到线段BD,
∴BD=BC,∠CBD=60°,
∴△BCD是等边三角形,
∴CD=BD,
∵线段BD平移到EF,
∴EF∥BD,EF=BD,
∴四边形BDFE是平行四边形,EF=CD,
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∴∠ABD=∠ABC-∠CBD=15°=∠ACD,
∴∠DFE=∠ABD=15°,∠AEF=∠ABD=15°,
∴∠AEF=∠ACD=15°,
∵∠CFE=∠A+∠AEF=30°+15°=45°,
∴∠CFD=∠CFE-∠DFE=45°-15°=30°,
∴∠A=∠CFD=30°,
在△AEF和△FCD中
$\left\{\begin{array}{l}{∠AEF=∠ACD}\\{∠A=∠CFD}\\{EF=CD}\end{array}\right.$
∴△AEF≌△FCD(AAS),
∴ΑE=CF;
(3)△CEF是等腰直角三角,
理由如下:
如图2,过点E作EG⊥CF于G,
∵∠CFE=45°,
∴∠FEG=45°,
∴EG=FG,
∵∠A=30°,∠AGE=90°,
∴EG=$\frac{1}{2}$AE,
∵ΑE=CF,
∴EG=$\frac{1}{2}$CF,
∴FG=$\frac{1}{2}$CF,
∴G为CF的中点,
∴EG为CF的垂直平分线,
∴EF=EC,
∴∠CEF=2∠FEG=90°,
∴△CEF是等腰直角三角形.
点评 本题为三角形的综合应用,涉及知识点有等腰三角形的性质、旋转和平移的性质、全等三角形的判定和性质及直角三角形的判定等.在(2)中构造三角形全等是解题的关键,在(3)中证得G为CF的中点是解题的关键.本题考查知识点较多,综合性很强,难度很大.

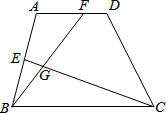 如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )
如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )| A. | 95 | B. | 100 | C. | 105 | D. | 110 |
| A. |  | B. |  | C. |  | D. |  |
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 该村人均耕地面积y与总人口x成正比例 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 当该村总人口为50人时,人均耕地面积为1公顷 |
| A. | a2•a5=a10 | B. | (a4)3=a12 | C. | (3a)2=6a2 | D. | a6÷a2=a3 |
 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN. 如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(2,0)
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(2,0)