题目内容
3.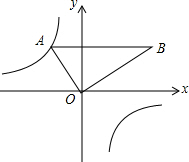 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.(1)求双曲线的解析式;
(2)把三角板AOB绕点A顺时针旋转,使得点O的对应点C落在x轴的负半轴上的对应线段为AD,试判断点D是否在双曲线上?请说明理由.
分析 (1)如图,先求出∠AOE=30°,再根据含30度的直角三角形三边的关系求出AE和OE,从而得到A点坐标,然后利用待定系数法求反比例函数解析式;
(2)利用旋转的性质得AC=AO,∠CAO=∠BAD,则可判断△AOC为等边三角形,得到∠CAO=∠BAD=60°,于是可判断点D在AC的延长线上,然后通过证明点A与点D关于原点对称得到点D是在双曲线上.
解答 解:(1)设AB与y轴相交于点E.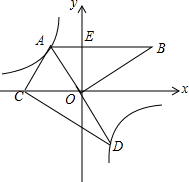
∵AB∥x轴,
∴∠AEO=90°
在Rt△AEO中,∠A=90°-30°=60°,
$OE=OA•sin60°=2×\frac{{\sqrt{3}}}{2}=\sqrt{3}$,$AE=OA•cos60°=2×\frac{1}{2}=1$.
∴点A的坐标为$({-1,\;\sqrt{3}})$,
设双曲线的解析式为$y=\frac{k}{x}({k≠0})$,$\sqrt{3}=\frac{k}{-1}$,$k=-\sqrt{3}$
∴双曲线的解析式为$y=-\frac{{\sqrt{3}}}{x}$;
(2)点D是在双曲线上.理由如下:
∵AB∥x轴,
∴∠AOC=∠BAO=60°
∵△ACD是由△AOB绕点A旋转得到的,
∴AO=AC,AB=AD
∴△AOC是等边三角形,
∴∠CAO=60°,即旋转角∠BAD=∠CAO=60°,
又∠BAO=60°,
∴点O在AD上,
在Rt△AOB中,∠B=30°,AB=2AO,
∴AD=2AO,AO=OD,
∴点D与点A关于点O中心对称.
∴点D在双曲线上.
点评 本题考查了用待定系数法求反比例函数的解析式:先设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);再把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;接着解方程,求出待定系数;然后写出解析式.解决(2)小题的关键是确定旋转角为60°.

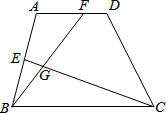 如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )
如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )| A. | 95 | B. | 100 | C. | 105 | D. | 110 |
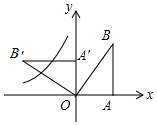 如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )
如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
| A. | b≥$\frac{5}{4}$ | B. | b≥1或b≤-1 | C. | b≥2 | D. | 1≤b≤2 |
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 该村人均耕地面积y与总人口x成正比例 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 当该村总人口为50人时,人均耕地面积为1公顷 |
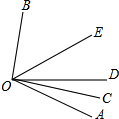 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线. 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)