题目内容
8.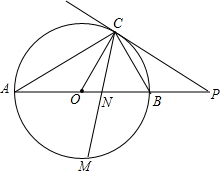 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.(1)求证:PC是⊙O的切线;
(2)求证:BC=$\frac{1}{2}$AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN•MC的值.
分析 (1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;
(2)AB是直径;故只需证明BC与半径相等即可;
(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MN•MC;代入数据可得MN•MC=BM2=8.
解答 (1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC=$\frac{1}{2}$AB.
(3)解:连接MA,MB,
∵点M是 $\widehat{AB}$的中点,
∴$\widehat{AM}$=$\widehat{BM}$,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴$\frac{BM}{MC}$=$\frac{MN}{BM}$.
∴BM2=MN•MC.
又∵AB是⊙O的直径,$\widehat{AM}$=$\widehat{BM}$,
∴∠AMB=90°,AM=BM.
∵AB=8,
∴BM=4 $\sqrt{2}$.
∴MN•MC=BM2=32.
点评 此题主要考查圆的切线的判定及圆周角定理的运用和相似三角形的判定和性质的应用,等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题.

 阅读快车系列答案
阅读快车系列答案| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
(2)根据上表,从这批羽毛球中任取一个,为优等品的概率约为0.9;
(3)小明认为,从这批羽毛球中抽取10个,优等品的数量至少为8个,他的说法正确吗?为什么?
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 对角线互相垂直 |
 如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求:
如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求: