题目内容
7．已知$\frac{a}{3}$=$\frac{b}{2}$≠0，求代数式$\frac{2a-b}{{a}^{2}-4{b}^{2}}$•（a+2b）的值．分析 设$\frac{a}{3}$=$\frac{b}{2}$=k≠0，可得，a=3k，b=2k，然后将原式转化为关于k的代数式，消元即可．
解答 解：设$\frac{a}{3}$=$\frac{b}{2}$=k≠0，
可得，a=3k，b=2k，
原式=$\frac{2a-b}{（a-2b）（a+2b）}$•（a+2b）=$\frac{2a-b}{a-2b}$，
把a=3k，b=2k代入上式，
原式=$\frac{2×3k-2k}{3k-2×2k}$=-4．
点评 本题考查了分式的化简求值，用k表示a、b是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．在方格纸中，每个方格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图甲中，每个小正方形的边长为1，以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化．
（1）根据图甲，填写下表，并计算出格点三角形面积的平均值．
（2）在图乙中，所给的方格纸大小与甲图一样，如果以线段CD为一边，做格点三角形，试填写下表，并计算出格点三角形面积的平均值．
（3）如果将图乙中格点三角形的面积用y来表示，频数用x来表示，根据你所填写的数据，猜想y与x之间存在何种函数关系？并求出该函数关系．
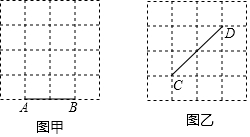
（1）根据图甲，填写下表，并计算出格点三角形面积的平均值．
| 格点三角形面积 | 1 | 2 | 3 | 4 |
| 频数 | 5 | 5 | 5 | 5 |
（3）如果将图乙中格点三角形的面积用y来表示，频数用x来表示，根据你所填写的数据，猜想y与x之间存在何种函数关系？并求出该函数关系．
如图，点A（m，m+1），B（m+3，m-1）是反比例函数y=$\frac{k}{x}$（x＞0）与一次函数y=ax+b的交点，求：
17．正方形具有而矩形不具有的性质是（ ）
| A． | 对边相等 | B． | 对角相等 | C． | 对角线相等 | D． | 对角线互相垂直 |