题目内容
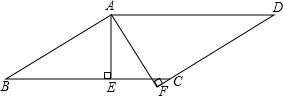
15. 已知:如图,△ABC中,AB=AC,CE⊥AE于E,CE=$\frac{1}{2}$BC,E在△ABC外,求证:∠ACE=∠B.
已知:如图,△ABC中,AB=AC,CE⊥AE于E,CE=$\frac{1}{2}$BC,E在△ABC外,求证:∠ACE=∠B.
分析 过A作AF⊥BC于点F,可证明△ABF≌△ACE,可证明结论.
解答  证明:
证明:
如图,过A作AF⊥BC于点F,
∵AB=AC,
∴BF=CF,
∵CE=$\frac{1}{2}$BC,
∴BF=CE,
∵CE⊥AE,
∴∠AFB=∠AEC=90°,
在Rt△ABF和Rt△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{BF=CE}\end{array}\right.$
∴Rt△ABF≌Rt△ACE(HL),
∴∠ACE=∠B.
点评 本题主要考查全等三角形的判定和性质,由条件构造三角形全等是解题的关键.

练习册系列答案
相关题目
5. 有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )
有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )
 有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )
有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.函数y=$\sqrt{3-x}$+$\frac{1}{x-2}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x<3且x≠2 | C. | x≤3且x≠2 | D. | x≠2 |
10.若关于x的不等式mx-n>0的解集是x<$\frac{1}{3}$,则关于x的不等式(m+n)x>n-m的解集是( )
| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<$\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
20.已知函数y=(k-3)x,y随x的增大而减小,则常数k的取值范围是( )
| A. | k>3 | B. | k<3 | C. | k<-3 | D. | k<0 |
7. 如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )
如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )
 如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )
如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )| A. | 65° | B. | 55° | C. | 35° | D. | 25° |
4.下列运算正确的是( )
| A. | x2•x6=x12 | B. | (-6x6)÷(-2x2)=3x3 | C. | 2a-3a=-a | D. | (x-2)2=x2-4 |