Question

某广场地面铺满了边长为36cm的正六边形地砖，现在向上抛掷半径为6的圆碟，圆碟落地后与地砖间的间隙不相交的概率大约是

 

．

Answer 1

考点：几何概率

专题：

分析：欲使圆碟不压地砖间的间隙，则圆碟的圆心必须落在与地砖同中心，且边与地砖边彼此平行，距离为6的小正六边形内，求出小正六边形的面积占大正六边形面积的多少即可．

解答：解：如图，作OC₁⊥A₁A₂，且C₁C₂=6，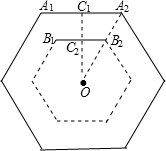
∵A₁A₂=A₂O=36，A₂C₁=18，
∴C₁O=18

3

，
∴C₂O=18

3

-6，
∴

小正六边形的面积

大正六边形的面积

=（

18 3 -6

18 3

）²=

28-6 3

27

∴圆碟落地后与地砖间的间隙不相交的概率大约是

28-6 3

27

，
故答案为：

28-6 3

27

．

点评：本题主要考查几何概率的计算，根据条件求出对应区域的面积是解决本题的关键，用到的知识点是概率公式，考查了学生的运算能力．