��Ŀ����
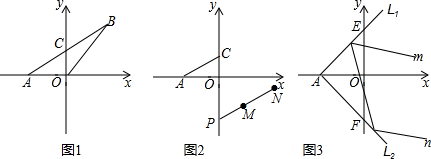
3����ͼ1��ƽ��ֱ������ϵ�У�A��-4��0����B��4��6����AB��y���ڵ�C������OB����1����C�����ꣻ
��2����ͼ2�����߶�ACƽ�����������õ�MN��C���Ӧ��N��m��-12�����ӳ�NM��y����P����m��ʾP�����ꣻ
��3����ͼ3����y������������һ��E��0��4����y�Ḻ��������һ�㶯��F������AE��AF����AE��AF�����������ཻ��ƽ�澵L1��L2��ƽ�澵L2��λ������F��λ�õĸı���ı䣮�Ƿ���ڵ�Fʹ���κ��䵽ƽ�澵L1��L2�ϵĹ���m����ƽ�澵L1��L2�����η�����������m�뷴�����n����ƽ�еģ������ڣ������F�����ꣻ�������ڣ���˵�����ɣ���˵����ƽ�澵������ߵĹ����ǣ�������ߺͷ��������ƽ�澵���еĽ���ȣ�
���� ��1����ֱ��AB�Ľ���ʽΪy=kx+b����A��B����������k��b��ֵ��ȷ��������ʽ���������C�����ꣻ
��2����ƽ�Ƶ����ʵõ�ֱ��MN��ֱ��ACб����ȣ���ʾ��MN���̣���x=0��ʾ��y��ֵ�����ɱ�ʾ��P���ꣻ
��3��������֪�����ó���EAF=90�㣬Ȼ�����ֱ��AE�Ľ���ʽ������ֱ��AE�Ľ���ʽ�����ֱ��AF�Ľ���ʽ���Ӷ����F�����꣮
���  �⣺��1����ͼ1����ֱ��AB�Ľ���ʽΪy=kx+b��
�⣺��1����ͼ1����ֱ��AB�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{-4k+b=0}\\{4k+b=6}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=$\frac{3}{4}$x++3��
��x=0����y=3��
��C���������0��3����
��2����ͼ2���߽��߶�ACƽ�����������õ�MN��
����ֱ��MN�Ľ���ʽΪy=$\frac{3}{4}$x+n��
�ߵ�N��m��-12����
��-12=$\frac{3}{4}$m+n��
��n=-12-$\frac{3}{4}$m��
��ֱ��MN�Ľ���ʽΪy=$\frac{3}{4}$x+n��y��Ľ�������Ϊ��0��n����
��P��������0��-12-$\frac{3}{4}$m����
��3����ͼ3�����������m�뷴�����n����ƽ�У�
���1+��2=180�㣬
���3+��4+��5+��6=180�㣬
�ߡ�3=��4����5=��6��
���3+��5=90�㣬
���EAF=90�㣬
��A��-4��0����E��0.4����
��ֱ��AE�Ľ���ʽΪy=x+4��
����ֱ��AF�Ľ���ʽΪy=-x+a��
��A��-4��0����
��4+a=0��
��a=-4��
��F��0��-4����
���� ���⿼����ƽ���ߵ��ж������ʣ�����ֱ�ߴ�ֱ�����ʣ�����ϵ������һ�κ����Ľ���ʽ��ֱ����������Ľ���ȣ���������ƽ���ߵ����ʺ�ֱ�ߴ�ֱ�������ǽ���Ĺؼ���

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�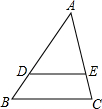 ��ͼ����ABC�У���D��E�ֱ���AB��AC���ϣ�DE��BC����AD��AB=3��4����ABC�����Ϊ
��ͼ����ABC�У���D��E�ֱ���AB��AC���ϣ�DE��BC����AD��AB=3��4����ABC�����Ϊ16�����ı���DBCE�������������
| A�� | 9 | B�� | 12 | C�� | 4 | D�� | 7 |
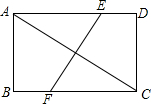 ��ͼ������ABCD�У�AB=3��BC=4�����������۵���ʹ��C�͵�A�غϣ����ۺ�EF�ij�Ϊ��������
��ͼ������ABCD�У�AB=3��BC=4�����������۵���ʹ��C�͵�A�غϣ����ۺ�EF�ij�Ϊ��������| A�� | $\frac{15}{4}$ | B�� | $\frac{15}{8}$ | C�� | 15 | D�� | 16 |
 ��1����ͼ����֪��1=��2����֤��a��b��
��1����ͼ����֪��1=��2����֤��a��b��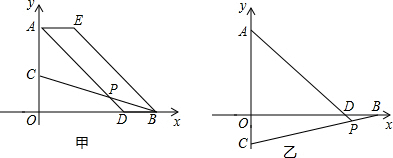
 ��ͼ��ʾ������ֽƬABCD�У�AB=5cm����E��BC�ϣ���AE=EC������ֽƬ��AE�۵�����Bǡ����AC�ϵĵ�B���غϣ���AC=10 cm��
��ͼ��ʾ������ֽƬABCD�У�AB=5cm����E��BC�ϣ���AE=EC������ֽƬ��AE�۵�����Bǡ����AC�ϵĵ�B���غϣ���AC=10 cm�� ��ͼ����֪��ABC��
��ͼ����֪��ABC��