题目内容
12．
如图，已知△ABC，（1）作∠BAC的角平分线交于BC于点D（要求尺规作图，不写作法）；
（2）若AB=AC=5，BC=6，求AD的长．
分析 （1）直接利用角平分线的作法得出AD即可；
（2）利用等腰三角形的性质结合勾股定理得出AD的长．
解答 
解：（1）如图所示：AD即为所求；
（2）∵AB=AC=5，AD平分∠BAC，
∴AD⊥BC，且BD=DC=$\frac{1}{2}$BC=3，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4．
点评 此题主要考查了基本作图以及等腰三角形的性质和勾股定理，得出BD=DC，AD⊥BC是解题关键．
练习册系列答案
相关题目
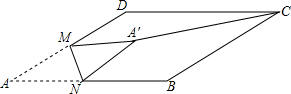如图，在平行四边形ABCD中，∠BCD=30°，BC=4，CD=3$\sqrt{3}$，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是5．
17．-2的绝对值是（ ）
| A． | 2 | B． | -2 | C． | -$\frac{1}{2}$ | D． | ±2 |
4．下面是四种车的车标，其中既是中心对称又是轴对称图案的是（ ）
| A． |  | B． |  | C． |  | D． |  |