题目内容
9.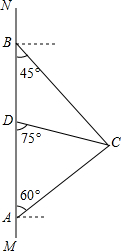 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号,已知A、B两船相距100($\sqrt{3}+1$)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号,已知A、B两船相距100($\sqrt{3}+1$)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.(1)求出A与C间的距离AC;
(2)已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救故障船C,在去营救的途中无触暗礁危险.
(填“有”或“无”,不必说明理由,参考数据:$\sqrt{2}≈1.41,\sqrt{3}≈1.73$)
分析 (1)作CE⊥AB,设AE=x海里,则BE=CE=$\sqrt{3}$x海里.根据AB=AE+BE=x+$\sqrt{3}$x=100($\sqrt{3}$+1),求得x的值后即可求得AC的长;
(2)过点D作DF⊥AC于点F,设AF=y,则DF=CF=$\sqrt{3}$y,根据AC=AF+FC得出AC=y+$\sqrt{3}$y=200,求出y的值,再根据AD的长和∠DAF的度数,求出线段DF的长,然后与100比较即可得到答案.
解答  解:(1)如图,作CE⊥AB,
解:(1)如图,作CE⊥AB,
由题意得:∠ABC=45°,∠BAC=60°,
设AE=x海里,
在Rt△AEC中,CE=AE•tan60°=$\sqrt{3}$x;
在Rt△BCE中,BE=CE=$\sqrt{3}$x.
则AE+BE=x+$\sqrt{3}$x=100($\sqrt{3}$+1),
解得:x=100.
AC=2x=200.
答:A与C之间的距离AC为200海里.
(2)过点D作DF⊥AC于点F,
在△ACD中,∠DAC=60°,∠ADC=75°,则∠ACD=45°,
设AF=y,则DF=CF=$\sqrt{3}$y,
∴AC=y+$\sqrt{3}$y=200,
解得:y=100($\sqrt{3}$-1),
∴AD=2y=200($\sqrt{3}$-1),
∴DF=$\sqrt{3}$AF=$\sqrt{3}$×100($\sqrt{3}$-1)≈126.3海里,
∵126.3>100,
∴巡逻船A沿直线AC航线,在去营救的途中无触暗礁危险.
故答案为:无.
点评 本题考查了解直角三角形的应用-方向角,关键是根据题意作出辅助线,构造直角三角形,利用直角三角形的边角关系进行求解.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
17.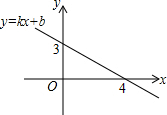 已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )
已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )
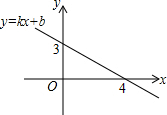 已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )
已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )| A. | x>3 | B. | x>4 | C. | x<3 | D. | x<4 |
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 矩形 | D. | 等腰梯形 |
3.已知$\frac{3x-3}{(x+1)(x-2)}$=$\frac{A}{x+1}$+$\frac{B}{x-2}$,则实数A,B分别为( )
| A. | 2,-1 | B. | -2,1 | C. | -2,-1 | D. | 2,1 |
4.下列分解因式正确的是( )
| A. | x2-x-2=(x-1)(x+2) | B. | -a2+a-$\frac{1}{4}$=$-\frac{1}{4}(2a-1)^{2}$ | ||
| C. | a(x-y)-b(y-x)=(x-y)(a-b) | D. | x2-4+2x=(x+2)(x-2)+2x |