题目内容
18.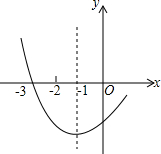 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②a+b+c<0;③2a-b=0; ④4a+2b+c<0;⑤若(-5,y1),$({\frac{5}{2},{y_2}})$是抛物线上两点,则y1>y2.其中说法正确的是①③⑤.
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②a+b+c<0;③2a-b=0; ④4a+2b+c<0;⑤若(-5,y1),$({\frac{5}{2},{y_2}})$是抛物线上两点,则y1>y2.其中说法正确的是①③⑤.
分析 根据开口方向确定a的符号,根据抛物线与y轴的交点确定c的符号,根据对称轴确定b的符号,判断①③;利用图象得出与x轴的另一交点,进而得出a+b+c=0,即可判断②,x=2时,y>0,判断④;根据函数增减性,判断⑤.
解答 解:∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=-1,
∴-$\frac{b}{2a}$=-1,
∴b=2a>0,
∴abc<0,
故①正确;
∵对称轴为x=-1,且过点(-3,0),
∴图象一定过(1,0)点,
则a+b+c=0,故②错误;
∵b=2a,
∴2a-b=0,
故③正确;
∵抛物线的对称轴为x=-1,且过点(-3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>-1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故④错误;
∵(-5,y1)关于直线x=-1的对称点的坐标是(3,y1),
又∵当x>-1时,y随x的增大而增大,3>$\frac{5}{2}$,
∴y1>y2,
故⑤正确.
故答案为:①③⑤.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键.重点把握抛物线的对称性.

练习册系列答案
相关题目
 如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为4.
如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为4. 如图,沿所画线折叠能形成一个立体图形,它的名称是三棱柱.
如图,沿所画线折叠能形成一个立体图形,它的名称是三棱柱.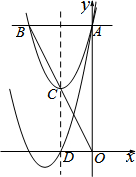 如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.
如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.