题目内容
3.对a,b定义一种新运算M,规定M(a,b)=$\frac{2ab}{a-b}$,这里等式右边是通常的四则运算,例如:M(2,3)=$\frac{2×2×3}{2-3}$=-12.(1)如果M(2x,1)=M(1,-1),求实数x的值;
(2)若令y=M(x+$\frac{3}{2}$,x-$\frac{1}{2}$),则y是x的函数,当自变量x在-1≤x≤2的范围内取值时,函数值y为整数的个数记为k,求k的值.
分析 (1)根据定义新运算的计算方法列出方程求得x的数值即可;
(2)根据定义新运算的计算方法列出二次函数解析式,进一步利用x的取值范围,得出y的取值范围,求得y的整数值,进一步确定k的值即可.
解答 解:(1)∵M(2x,1)=M(1,-1),
∴$\frac{4x}{2x-1}$=$\frac{-2}{2}$,
解得:x=$\frac{1}{6}$;
经检验:x=$\frac{1}{6}$是原分式方程的解.
(2)y=M(x+$\frac{3}{2}$,x-$\frac{1}{2}$)
=$\frac{2(x+\frac{3}{2})(x-\frac{1}{2})}{(x+\frac{3}{2})-(x-\frac{1}{2})}$
=x2+x-$\frac{3}{4}$=(x+$\frac{1}{2}$)2-1,
∵当x=-$\frac{1}{2}$时,y=-1,当x=2时,y=5$\frac{1}{4}$,
∴当-1≤x≤2时,y的整数值由-1,0,1,2,3,4,5这7个数;
即k=7.
点评 此题考查二次函数的性质,解分式方程,理解定义新运算的方法,掌握二次函数的性质以及解分式方程的步骤与方法是解决问题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
13.如图,它们是一个物体的三视图,该物体的形状是( )


| A. | 长方体 | B. | 正方体 | C. | 圆柱 | D. | 圆锥 |
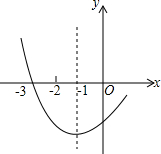 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②a+b+c<0;③2a-b=0; ④4a+2b+c<0;⑤若(-5,y1),$({\frac{5}{2},{y_2}})$是抛物线上两点,则y1>y2.其中说法正确的是①③⑤.
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②a+b+c<0;③2a-b=0; ④4a+2b+c<0;⑤若(-5,y1),$({\frac{5}{2},{y_2}})$是抛物线上两点,则y1>y2.其中说法正确的是①③⑤. 已知一个正方体所有相对的面上两数之和相等.如图是它的展开图,请填出图中空白正方形中的数.
已知一个正方体所有相对的面上两数之和相等.如图是它的展开图,请填出图中空白正方形中的数. 已知二次函数y=-x2-2x+3
已知二次函数y=-x2-2x+3