题目内容
8.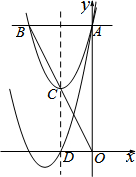 如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.
如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.
分析 先确定A(0,8),则表示出B点坐标(-b,8)(b>0),利用点C为OB的中点可得到C(-$\frac{1}{2}$b,4),根据抛物线的顶点坐标公式得到$\frac{4×8-{b}^{2}}{4}$=4,解得b=4或b=-4(舍去),所以抛物线解析式为y=x2+4x+8=(x+2)2+4,则D(-2,0),然后设平移后的抛物线解析式为y=x2+mx+n,再把A点和D点坐标代入得到m、n的方程组,接着解方程组求出m、n即可.
解答 解:当x=0时,y=x2+bx+8=8,则A(0,8),
∵AB∥x轴,
∴B点的纵坐标为8,
当y=8时,x2+bx+8=8,解得x1=0,x2=-b,
∴B(-b,8)(b>0),
∵点C为OB的中点,
∴C(-$\frac{1}{2}$b,4),
∵C点为抛物线的顶点,
∴$\frac{4×8-{b}^{2}}{4}$=4,解得b=4或b=-4(舍去),
∴抛物线解析式为y=x2+4x+8=(x+2)2+4,
∴抛物线的对称轴为直线x=-2,
∴D(-2,0),
设平移后的抛物线解析式为y=x2+mx+n,
把A(0,8),D(-2,0)代入得$\left\{\begin{array}{l}{n=8}\\{4-2m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=6}\\{n=8}\end{array}\right.$,
所以平移后的抛物线解析式为y=x2+6x+8.
故答案为y=x2+6x+8.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了抛物线的几何变换.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.数3.14,$\sqrt{2}$,$\frac{π}{2}$,0.323232…,$\frac{1}{7}$,$\sqrt{9}$,$\frac{22}{7}$,1+$\sqrt{2}$中,无理数的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
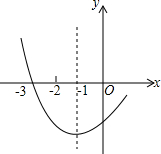 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②a+b+c<0;③2a-b=0; ④4a+2b+c<0;⑤若(-5,y1),$({\frac{5}{2},{y_2}})$是抛物线上两点,则y1>y2.其中说法正确的是①③⑤.
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②a+b+c<0;③2a-b=0; ④4a+2b+c<0;⑤若(-5,y1),$({\frac{5}{2},{y_2}})$是抛物线上两点,则y1>y2.其中说法正确的是①③⑤.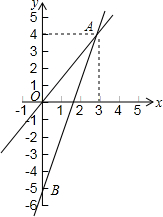 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB. 已知二次函数y=-x2-2x+3
已知二次函数y=-x2-2x+3