题目内容
10.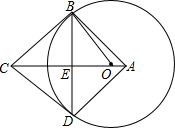 如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=$\frac{3}{5}$.求证:CB是⊙O的切线.
如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=$\frac{3}{5}$.求证:CB是⊙O的切线.
分析 连接OD,可得OB=OD,由AB=AD,得到AE垂直平分BD,在直角三角形BOE中,利用锐角三角函数定义求出OE的长,根据勾股定理求出BE的长,由OC-OE求出CE的长,再利用勾股定理求出BC的长,利用勾股定理逆定理判断得到BC与OB垂直,即可确定出BC为圆O的切线.
解答  证明:连接OD,可得OB=OD,
证明:连接OD,可得OB=OD,
∵AB=AD,
∴AE垂直平分BD,
在Rt△BOE中,OB=3,cos∠BOE=$\frac{3}{5}$,
∴OE=$\frac{9}{5}$,
根据勾股定理得:BE=$\sqrt{B{O}^{2}-O{E}^{2}}$=$\frac{12}{5}$,CE=OC-OE=$\frac{16}{5}$,
在Rt△CEB中,BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=4,
∵OB=3,BC=4,OC=5,
∴OB2+BC2=OC2,
∴∠OBC=90°,即BC⊥OB,
则BC为圆O的切线.
点评 此题考查了切线的判定,勾股定理及逆定理,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.下列各组中的四条线段成比例的是( )
| A. | a=$\sqrt{2}$,b=3,c=2,d=$\sqrt{3}$ | B. | a=4,b=6,c=5,d=10 | ||
| C. | a=2,b=$\sqrt{5}$,c=2$\sqrt{3}$,d=$\sqrt{15}$ | D. | a=2,b=3,c=4,d=1 |
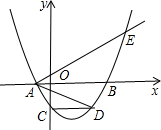 如图,二次函数y=ax2-2amx-3am2(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
如图,二次函数y=ax2-2amx-3am2(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.