题目内容
14.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是整点.若整点P(m+2,2m-1)在第四象限,则m的值为-1或0.分析 根据第四象限内点的横坐标是正数,纵坐标是负数列出不等式组,然后求解即可.
解答 解:∵点P(m+2,2m-1)在第四象限,
∴$\left\{\begin{array}{l}{m+2>0}\\{2m-1<0}\end{array}\right.$
解得:-2<m<$\frac{1}{2}$,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为-1或0.
故答案为:-1或0.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
4.下列命题是错误的是( )
| A. | 四条边相等的四边形是菱形 | B. | 对角线垂直的平行四边形是菱形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 对角线相等的平行四边形是矩形 |
5.用不等式表示“x的2倍与3的差不大于8”为( )
| A. | 2x-3<8 | B. | 2x-3>8 | C. | 2x-3≥8 | D. | 2x-3≤8 |
12.化简计算$\sqrt{99999×99999+199999}$的结果是( )
| A. | 100000 | B. | 10000 | C. | 1000 | D. | 以上答案都不对 |
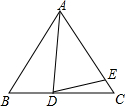 如图,在△ABC中,∠B=∠C,点D是BC边上一点,连接AD,作∠ADE=∠AED,交AC于E,求证:∠CDE=$\frac{1}{2}$∠BAD.
如图,在△ABC中,∠B=∠C,点D是BC边上一点,连接AD,作∠ADE=∠AED,交AC于E,求证:∠CDE=$\frac{1}{2}$∠BAD.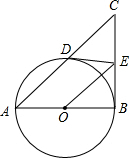 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE 如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为9.
如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为9.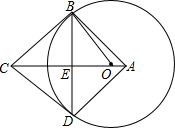 如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=$\frac{3}{5}$.求证:CB是⊙O的切线.
如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=$\frac{3}{5}$.求证:CB是⊙O的切线.