题目内容

15．已知x2+2（n+1）x+4n是一个关于x的完全平方式，则常数n=1．

分析 利用x2+2（n+1）x+4n是一个关于x的完全平方式，则x2+2（n+1）x+4n=0的判别式等于0，据此即可求得n的值．

解答 解：根据题意得：[2（n+1）]2-4×4n=0，
解得：n=1．
故答案为：1．

点评 本题考查了完全平方式的定义以及根的判别式，得出判别式等于0是关键．

练习册系列答案
相关题目
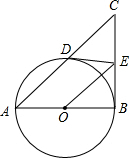5．如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D作⊙O的切线交BC于点E，连接OE
（1）证明OE∥AD；
（2）①当∠BAC=45°时，四边形ODEB是正方形．
     ②当∠BAC=30°时，AD=3DE．
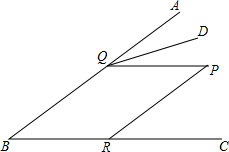6．如图，点P在∠ABC内，点Q，R分别在∠ABC的边BA，BC上，QD平分∠AQP，连接PQ，PR．若∠PRC=∠B，∠P=50°，求∠PQD的度数．
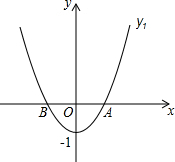3．如图，在平面直角坐标系中，抛物线y1=x2-1与x轴交于点A和点B（点A在点B的右侧），抛物线y2的解析式为y2=$\frac{1}{1-n}$（x-n）2+n-1（n≠1，直线y3的解析式为y3=x-2．
（1）试通过计算说明抛物线y2与直线y3均过点A；
（2）若抛物线y2与x轴的另一交点为C，且有BC=2AB，请求出此时y2的解析式；
（3）当n≤0时，已知对于x的任意同一个值，所对应三个函数的函数值为y1，y2，y3，请画出它们的大致图象后猜想y1，y2，y3的大小关系并给出证明．
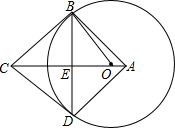10．如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=$\frac{3}{5}$．求证：CB是⊙O的切线．
20．下列说法正确的是（　　）
A．两个等边三角形一定全等B．腰对应相等的两个等腰三角形全等
C．形状相同的两个三角形全等D．全等三角形的面积一定相等
7．有一个两位数，它的十位数字与个位数字之和为6，则符合条件的两位数有（　　）
A．5个B．6个C．7个D．8个
4．如图1，已知：正比例函数y=k1x的图象与反比例函数y=$\frac{a}{x}$的图象交于点A（3，2）、B（m，n）．我们可以发现：反比例函数的图象是一个关于原点中心对称的图形．你可以利用这一结论解决问题．
（1）填空：k1=$\frac{2}{3}$，a=6，m=-3，n=-2；
（2）利用所给函数图象，写出不等式k1x＜$\frac{a}{x}$的解集：x＜-3或0＜x＜3；
（3）如图2，正比例函数y=k2x（k2≠k1）的图象与反比例函数y=$\frac{a}{x}$的图象交于点P、Q，以A、B、P、Q为顶点的四边形记为代号“图形※”．
①试说明：图形※一定是平行四边形，但不可能是正方形；
②如图3，当P点在A点的左上方时，过P作直线PM⊥y轴于点M，过点A作直线AN⊥x轴于点N，交直线PM于点D，
若四边形OADP的面积为6．求P点的坐标．
5．化简：
（1）（2$\sqrt{12}$-3$\sqrt{\frac{1}{3}}$）×$\sqrt{6}$；        
（2）$\frac{x}{{x}^{2}-4}$-$\frac{1}{2x-4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网