题目内容
11.菱形的面积为120,其中较短的对角线为10,则菱形的周长为52.分析 先根据菱形的面积公式=两条对角线乘积的一半计算另一条对角线的长,利用勾股定理求菱形的边长,菱形的周长等于边长的4倍.
解答  解:如图,由已知得:S菱形=120,AC=10,
解:如图,由已知得:S菱形=120,AC=10,
则$\frac{1}{2}$AC•BD=120,
∴$\frac{1}{2}$×10BD=120,
BD=24,
∵四边形ABCD是菱形,
∴OA=$\frac{1}{2}$AC=5,OD=$\frac{1}{2}$BD=12,AC⊥BD,
在Rt△OAD中,由勾股定理得:AD=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴菱形的周长为:13×4=52;
故答案为:52.
点评 本题考查了菱形的性质,明确菱形的四边相等,且对角线互相平分垂直,在菱形中常根据勾股定理列式求对角线或边长,因此熟练掌握菱形的性质是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
4.已知M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直,平行 | D. | 平行,垂直 |
5.下列说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角; ③过一点有且仅有一条直线与己知直线平行; ④两点之间的距离是两点间的线段; ⑤若AB=BC,则点B为线段AC的中点;⑥不相交的两条直线叫做平行线.其中正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.下列命题是真命题的是( )
| A. | 两个锐角的和一定是钝角 | |
| B. | 两条平行线被第三条直线所截,同旁内角的平分线互相垂直 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 直线外一点到这条直线的垂线段,叫做这点到该直线的距离 |
 已知:如图,∠BAP+∠APD=180°,∠1=∠2.求证:AE∥FP.
已知:如图,∠BAP+∠APD=180°,∠1=∠2.求证:AE∥FP.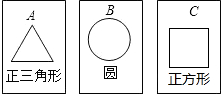 如图,有三张背面完全相同的纸牌A、B、C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
如图,有三张背面完全相同的纸牌A、B、C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.