题目内容
5.若$\frac{1-3x}{{x}^{2}-1}$=$\frac{M}{x+1}$+$\frac{N}{x-1}$,求M,N的值.分析 已知等式右边通分并利用同分母分式的加法法则计算,再利用分式相等的条件求出M与N的值即可.
解答 解:已知等式整理得:$\frac{1-3x}{{x}^{2}-1}$=$\frac{M(x-1)+N(x+1)}{{x}^{2}-1}$,
可得1-3x=(M+N)x+N-M,即$\left\{\begin{array}{l}{M+N=-3}\\{N-M=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{M=-2}\\{N=-1}\end{array}\right.$.
点评 此题考查了分式的加减法,以及分式相等的条件,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.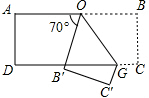 如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
 如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
14.如果二次函数y=x2-6x+8在x的一定取值范围内有最大值(或最小值)为3,满足条件的x的取值范围可以是( )
| A. | -1≤x≤5 | B. | 1≤x≤6 | C. | -2≤x≤4 | D. | -1≤x≤1 |
 如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,CD=2.4,则点C到直线AB的距离等于2.4.
如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,CD=2.4,则点C到直线AB的距离等于2.4. 如图,是将两个边长分别为和的正方形拼在一起,B、C、G三点在同一直线上.连接BD和BF,若两正方形的边长满足a+b=6,ab=6,你能求出阴影部分的面积S阴吗?
如图,是将两个边长分别为和的正方形拼在一起,B、C、G三点在同一直线上.连接BD和BF,若两正方形的边长满足a+b=6,ab=6,你能求出阴影部分的面积S阴吗?