题目内容
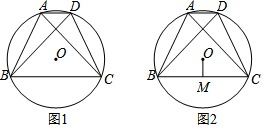
3.研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半,如图1,己知四边形ABCD内接于⊙O,对角线AC=BD,且AC⊥BD(1)求证:AB=CD;
(2)若⊙O的半径为8,弧BD的度数为120°,求四边形ABCD的面积;
(3)如图2,作OM⊥BC于M,请猜测OM与AD的数量关系,并证明你的结论.
分析 (1)根据弦、弧、圆心角的关系证明;
(2)根据弧BD的度数为120°,得到∠BOD=120°,利用解直角三角形的知识求出BD,根据题意计算即可;
(3)连结OB、OC、OA、OD,作OE⊥AD于E,如图3,根据垂径定理得到AE=DE,再利用圆周角定理得到∠BOM=∠BAC,∠AOE=∠ABD,再利用等角的余角相等得到∠OBM=∠AOE,则可证明△BOM≌△OAE得到OM=AE,证明结论.
解答 (1)证明:∵AC=BD,
∴$\widehat{AC}$=$\widehat{BD}$,
则$\widehat{AB}$=$\widehat{DC}$,
∴AB=CD;
(2)解:连接OB、OD,作OH⊥BD于H,
∵弧BD的度数为120°,
∴∠BOD=120°,
∴∠BOH=60°,
则BH=$\frac{\sqrt{3}}{2}$OB=4$\sqrt{3}$,
∴BD=8$\sqrt{3}$,
则四边形ABCD的面积=$\frac{1}{2}$×AC×BD=96;
(3)AD=2OM,
连结OB、OC、OA、OD,作OE⊥AD于E,如图2,
∵OE⊥AD,
∴AE=DE,
∵∠BOC=2∠BAC,
而∠BOC=2∠BOM,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠AOE,
在△BOM和△OAE中,
$\left\{\begin{array}{l}{∠OMB=∠OEA}\\{∠OBM=∠OAE}\\{OB=OA}\end{array}\right.$,
∴△BOM≌△OAE,
∴OM=AE,
∴AD=2OM.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、垂径定理、等腰三角形的性质和矩形的性质、会利用三角形全等解决线段相等的问题是解题的关键.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | -1≤x≤5 | B. | 1≤x≤6 | C. | -2≤x≤4 | D. | -1≤x≤1 |
| A. | 火车开到月球上 | B. | 在地面上向空中抛出的石子会落下 | ||
| C. | 2018年元旦当天杭州会下雨 | D. | 早晨太阳从东方升起 |
| A. | 48(1-x)2=36 | B. | 48(1+x)2=36 | C. | 36(1+x)2=48 | D. | 36(1-x)2=48 |
 如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,CD=2.4,则点C到直线AB的距离等于2.4.
如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,CD=2.4,则点C到直线AB的距离等于2.4.