Question

4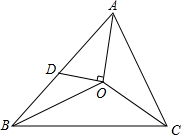．如图，O是△ABC的三条角平分线的交点，过点O作AO的垂线交AB于点D，求证：△OBD∽△CBO．

Answer 1

分析 根据三角形内心的性质得∠1=$\frac{1}{2}$∠BAC，∠2=∠4，∠3=$\frac{1}{2}$∠ACB，则利用三角形内角和定理得到∠1+∠2+∠3=90°，则∠BOC=180°-（∠2+∠3）=90°+∠1，再根据三角形外角性质得∠BDO=∠DOA+∠1，于是得到∠BDO=∠BOC，然后根据有两组角对应相等的两个三角形相似可判断△OBD∽△CBO．

解答 证明：如图，
∵O是△ABC的三条角平分线的交点，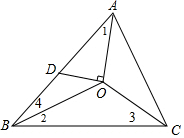
∴∠1=$\frac{1}{2}$∠BAC，∠2=∠4，∠3=$\frac{1}{2}$∠ACB，
∴∠1+∠2+∠3=90°，
即∠2+∠3=90°-∠1，
而∠BOC=180°-（∠2+∠3）=90°+∠1，
∵∠BDO=∠DOA+∠1，
而AO⊥OD，
∴∠DOA=90°，
∴∠BDO=∠BOC，
而∠4=∠2，
∴△OBD∽△CBO．

点评 本题考查了相似三角形的判定与性质：有两组角对应相等的两个三角形相似．也考查了三角形的内心的性质．