题目内容
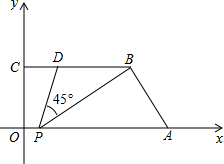 如图,在平面直角坐标系中A(6,0),B(5,3),C(0,3),D(1,3),点P为线段OA上一点且∠BPD=45°,则点P坐标为
如图,在平面直角坐标系中A(6,0),B(5,3),C(0,3),D(1,3),点P为线段OA上一点且∠BPD=45°,则点P坐标为考点:圆的综合题
专题:综合题
分析:作BD的垂直平分线交BD于H,交OA于N,在HN上截取HM=
BD,以M点为圆心,BM为半径作⊙O交OA于P1,P2,连接MP1,如图,由MH⊥BD,MH=
BD可判断△BDM为等腰直角三角形,则∠BMD=90°,根据圆周角定理得∠BP1D=∠BP2D=
∠BMD=45°,即P1点和P2点为满足条件的点;再由D(1,3),B(5,3)得到BC∥OA,BD=4,由于MH垂直平分BD,易得H(3,3),N(3,0),M(3,1),然后根据勾股定理在Rt△BMH中计算出BM=2
,在Rt△MNP1中计算出NP1=
,
∴NP2=NP1=
,则OP1=ON-NP1=3-
,OP2=ON+NP2=3+
,易得P1(3-
,0),P2(3+
,0),所以P点坐标为(3-
,0)或(3+
,0).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 7 |
∴NP2=NP1=
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
解答:解: 作BD的垂直平分线交BD于H,交OA于N,在HN上截取HM=
作BD的垂直平分线交BD于H,交OA于N,在HN上截取HM=
BD,以M点为圆心,BM为半径作⊙O交OA于P1,P2,连接MP1,如图,
∵MH⊥BD,MH=
BD,
∴△BDM为等腰直角三角形,
∴∠BMD=90°,
∴∠BP1D=∠BP2D=
∠BMD=45°,
∵D(1,3),B(5,3),
∴BC∥OA,BD=4,
∵MH垂直平分BD,
∴H(3,3),N(3,0),M(3,1),
在Rt△BMH中,BM=
=
=2
,
在Rt△MNP1中,NP1=
=
=
,
∴NP2=NP1=
,
∴OP1=ON-NP1=3-
,OP2=ON+NP2=3+
,
∴P1(3-
,0),P2(3+
,0),
即P点坐标为(3-
,0)或(3+
,0).
故答案为(3-
,0)或(3+
,0).
 作BD的垂直平分线交BD于H,交OA于N,在HN上截取HM=
作BD的垂直平分线交BD于H,交OA于N,在HN上截取HM=| 1 |
| 2 |
∵MH⊥BD,MH=
| 1 |
| 2 |
∴△BDM为等腰直角三角形,
∴∠BMD=90°,
∴∠BP1D=∠BP2D=
| 1 |
| 2 |
∵D(1,3),B(5,3),
∴BC∥OA,BD=4,
∵MH垂直平分BD,
∴H(3,3),N(3,0),M(3,1),
在Rt△BMH中,BM=
| BH2+MH2 |
| 22+22 |
| 2 |
在Rt△MNP1中,NP1=
| MP12-MN2 |
(2
|
| 7 |
∴NP2=NP1=
| 7 |
∴OP1=ON-NP1=3-
| 7 |
| 7 |
∴P1(3-
| 7 |
| 7 |
即P点坐标为(3-
| 7 |
| 7 |
故答案为(3-
| 7 |
| 7 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理、垂径定理和等腰直角三角形的性质;会运用勾股定理计算线段的长;理解坐标与图形性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
 已知,M是△ABC内的一点,MD⊥BC,ME⊥AC,MF⊥AB,且BD=BF,CD=CE,求证:AE=AF.
已知,M是△ABC内的一点,MD⊥BC,ME⊥AC,MF⊥AB,且BD=BF,CD=CE,求证:AE=AF. 如图,把长方形纸片ABCD折叠,使A、C重合,EF为折痕,若AB=9,BC=3,求BF的长度.
如图,把长方形纸片ABCD折叠,使A、C重合,EF为折痕,若AB=9,BC=3,求BF的长度. 我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
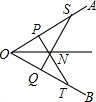 如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.
如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB. 如图,已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=40°,则∠AOC=
如图,已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=40°,则∠AOC=