题目内容
6.若抛物线y=ax2+bx+c经过(0,1)和(2,-3)两点,且开口向下,对称轴在y轴的左侧,则a的取值范围是( )| A. | a<0 | B. | -2<a<0 | C. | -$\frac{2}{3}$<a<0 | D. | -1<a<0 |
分析 首先将已知两点的坐标代入二次函数的解析式,从而用a表示出b,然后根据对称轴的位置确定a的取值范围即可.
解答 解:分别将(0,1)和(2,-3)两点代入y=ax2+bx+c得:$\left\{\begin{array}{l}{c=1}\\{4a+2b+1=-3}\end{array}\right.$,
∴b=-2-2a ①,
∵开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴-$\frac{b}{2a}$<0 ②,
把①代入②得-$\frac{-2-2a}{2a}$<0,
即$\frac{1+a}{a}$<0,
∵a<0,
∴1+a>0,
∴a>-1,
∴a的取值范围是-1<a<0,
故选D.
点评 本题考查了二次函数的性质,解题的关键是能够根据对称轴的位置确定a的取值范围,难度不大.

练习册系列答案
相关题目
16.若a2=9,$\root{3}{b}$=-2,则a+b=( )
| A. | -5 | B. | -11 | C. | -5 或-11 | D. | ±5或±11 |
11.下列函数的图象与y轴不相交的是( )
| A. | y=-x | B. | y=4x+1 | C. | y=$\frac{2}{x}$ | D. | y=x2+2x |
15.如果两个相似三角形的相似比是1:7,则它们的面积比等于( )
| A. | 1:$\sqrt{7}$ | B. | 1:7 | C. | 1:3.5 | D. | 1:49 |
16.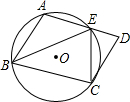 如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )
如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )
 如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )
如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=10,那么BC的长等于6.
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=10,那么BC的长等于6.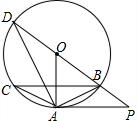 如图,⊙O是△ABC的外接圆,AB=AC,BD是⊙O的直径.PA∥BC,与DB的延长线交于点P.连结AD.
如图,⊙O是△ABC的外接圆,AB=AC,BD是⊙O的直径.PA∥BC,与DB的延长线交于点P.连结AD.