题目内容
1.计算:(1)$\sqrt{12}-2$sin60°+|1-$\sqrt{3}$|+20160
(2)(1-$\frac{1}{a-1}$)÷$\frac{{a}^{2}-4a+4}{{a}^{2}-a}$.
分析 (1)先对原式化简,再合并同类项即可解答本题;
(2)先将括号内的式子通分再与括号外的式子相除,将除法转化为乘法进行约分化简即可.
解答 解:(1)$\sqrt{12}-2$sin60°+|1-$\sqrt{3}$|+20160
=$2\sqrt{3}-2×\frac{\sqrt{3}}{2}+\sqrt{3}-1+1$
=$2\sqrt{3}-\sqrt{3}+\sqrt{3}-1+1$
=2$\sqrt{3}$;
(2)(1-$\frac{1}{a-1}$)÷$\frac{{a}^{2}-4a+4}{{a}^{2}-a}$
=$\frac{a-1-1}{a-1}×\frac{a(a-1)}{(a-2)^{2}}$
=$\frac{a-2}{a-1}×\frac{a(a-1)}{(a-2)^{2}}$
=$\frac{a}{a-2}$.
点评 本题考查分式的混合运算、实数的运算、零指数幂、特殊角的三角函数值,解题的关键是明确它们各自的计算方法,注意去绝对值符号时,是否要变号.

练习册系列答案
相关题目
11.如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 都有可能 |
12.计算$\frac{{a}^{2}}{{b}^{3}}$$•\frac{2{b}^{2}}{3{a}^{2}}$的结果是( )
| A. | $\frac{2a}{3}$ | B. | $\frac{2b}{3}$ | C. | $\frac{2}{b}$ | D. | $\frac{2}{3b}$ |
6.若抛物线y=ax2+bx+c经过(0,1)和(2,-3)两点,且开口向下,对称轴在y轴的左侧,则a的取值范围是( )
| A. | a<0 | B. | -2<a<0 | C. | -$\frac{2}{3}$<a<0 | D. | -1<a<0 |
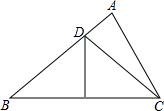 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.