题目内容
11.下列函数的图象与y轴不相交的是( )| A. | y=-x | B. | y=4x+1 | C. | y=$\frac{2}{x}$ | D. | y=x2+2x |
分析 由函数的性质可知:与y轴不相交,也就是x的取值不能为0,由此根据反函数的性质分析得出答案及可能.
解答 解:反比例函数的图象是双曲线,这两条曲线只能无限接近于两坐标轴,但不能与其相交,也就是图象与y轴不相交.
故选:C.
点评 此题考查二次函数得性质、一次函数的性质、反比例函数的性质,掌握反比例函数的图象是双曲线,这两条曲线只能无限接近于两坐标轴,但不能与其相交是解决问题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
1.若关于x的方程x2-4x+m+4=0有实数根,则m的取值范围是( )
| A. | m<0 | B. | m≤0 | C. | m>0 | D. | m≥0 |
19.下列运算中,正确的是( )
| A. | m2•m3=m6 | B. | (-m2)3=m6 | C. | -m2-2m2=-3m2 | D. | -3m-2=-$\frac{1}{9{m}^{2}}$ |
6.若抛物线y=ax2+bx+c经过(0,1)和(2,-3)两点,且开口向下,对称轴在y轴的左侧,则a的取值范围是( )
| A. | a<0 | B. | -2<a<0 | C. | -$\frac{2}{3}$<a<0 | D. | -1<a<0 |
3.下列式子正确的是( )
| A. | 3a2b+2ab2=5a3b3 | B. | 2-$\frac{2}{x-1}$=$\frac{2x-4}{x-1}$ | C. | (x-2)(-x+2)=x2-4 | D. | a2•a3+a6=2a6 |
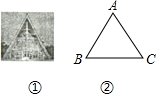 如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)
如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)