题目内容
18.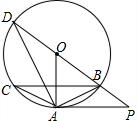 如图,⊙O是△ABC的外接圆,AB=AC,BD是⊙O的直径.PA∥BC,与DB的延长线交于点P.连结AD.
如图,⊙O是△ABC的外接圆,AB=AC,BD是⊙O的直径.PA∥BC,与DB的延长线交于点P.连结AD.(1)求证:PA是⊙O的切线;
(2)若tan∠ABC=$\frac{1}{2}$,BC=4,求BD与AD的长.
分析 (1)由垂径定理的推论可证明OA⊥BC,又因为PA∥BC,所以AP⊥OA,即PA是⊙O的切线;
(2)设BC和OA相较于点M,由已知条件易求AB的长,由圆周角定理定理可得△DAB是直角三角形,进而可求出BD,AD的长.
解答 (1)证明:∵AB=AC,
∴$\widehat{AB}=\widehat{AC}$,
∴OA⊥BC,
∵PA∥BC,
∴AP⊥OA,
即PA是⊙O的切线;
(2)∵AC=BC,
∴∠ABC=∠ACB,
∵BC=4,OM⊥BC,
∴BM=2,
∵tan∠ABC=$\frac{1}{2}$,
∴AB=$\sqrt{5}$,
∵∠D=∠ACB,tan∠ABC=$\frac{1}{2}$,
∴tan∠D=$\frac{1}{2}$,
∵BD是⊙O的直径,
∴∠BAD=90°,
∴AD=2$\sqrt{5}$,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5.
点评 本题考查了切线的判定、圆周角定理以及其推论的运用、垂径定理以及其推论的运用、勾股定理的运用,锐角三角的函数的运用,题目的综合性较强,难度中等,是一道不错的中考试题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若抛物线y=ax2+bx+c经过(0,1)和(2,-3)两点,且开口向下,对称轴在y轴的左侧,则a的取值范围是( )
| A. | a<0 | B. | -2<a<0 | C. | -$\frac{2}{3}$<a<0 | D. | -1<a<0 |
3.下列式子正确的是( )
| A. | 3a2b+2ab2=5a3b3 | B. | 2-$\frac{2}{x-1}$=$\frac{2x-4}{x-1}$ | C. | (x-2)(-x+2)=x2-4 | D. | a2•a3+a6=2a6 |
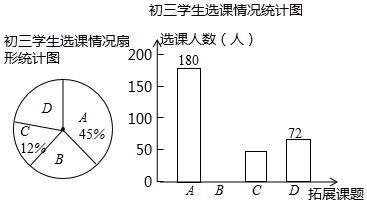



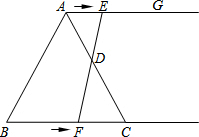 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.