Question

16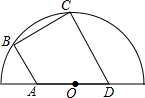．如图，四边形ABCD内接于半圆O，其中点A，D在直径上，点B，C在半圆弧上，AB∥CD，∠B=90°，若AO=3，∠BAD=120°，则BC=3$\sqrt{3}$．

Answer 1

分析 过O作OH⊥BC于H，得到BH=CH，过B作BM∥AD，得到四边形ADMB是平行四边形，根据平行四边形的性质得到BM=AD，根据平行线等分线段定理得到OD=OA=6，解直角三角形即可得到结论．

解答 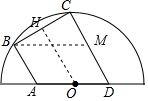解：过O作OH⊥BC于H，则BH=CH，
过B作BM∥AD，则四边形ADMB是平行四边形，
∴BM=AD，
∵∠B=90°，
∴∠C=90°，
∴AB∥OH∥CD，
∴OD=OA=6，
∴BM=6，
∵∠BAD=120°，
∴∠MBA=60°，
∴∠CBM=30°，
∴BC=$\frac{\sqrt{3}}{2}$BM=3$\sqrt{3}$．
故答案为：3$\sqrt{3}$．

点评 本题考查了圆周角定理，平行线的性质，平行四边形的判定和性质，解直角三角形，垂径定理，正确的作出辅助线是解题的关键．