题目内容
4. 如图,在⊙O中,直径CD交弦AB于点H,∠OBH=20°,∠C的度数为35°.
如图,在⊙O中,直径CD交弦AB于点H,∠OBH=20°,∠C的度数为35°.
分析 由“等弧所对的圆周角是所对的圆心角的一半”推知∠DOB=2∠C;则在直角△BOE中,利用“直角三角形的两个锐角互余”的性质解题.
解答 解:∵在⊙O中,直径CD垂直于弦AB,
∴$\widehat{AD}$=$\widehat{BD}$,
∴∠C=$\frac{1}{2}$∠BOH=$\frac{1}{2}$(90°-20°)=35°.
故答案为35°.
点评 本题考查了圆周角定理、垂径定理.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
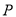 经过
经过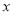 轴上一点
轴上一点 ,与y轴分别交于
,与y轴分别交于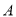 、
、 两点,连接
两点,连接 并延长分别交⊙
并延长分别交⊙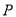 、
、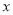 轴于点
轴于点 、
、 ,连接
,连接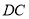 并延长交y轴于点
并延长交y轴于点 ,若点
,若点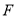 的坐标为(0,1),点
的坐标为(0,1),点 的坐标为(6,-1).
的坐标为(6,-1). ;
;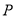 与
与 轴的位置关系,并说明理由;
轴的位置关系,并说明理由; 的半径的长.
的半径的长.
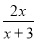 有意义,则
有意义,则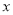 的取值范围是____________.
的取值范围是____________.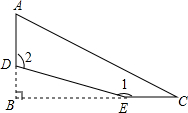 有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为105°.
有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为105°. 在正方形ABCD中,BD是对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH,PH.
在正方形ABCD中,BD是对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH,PH.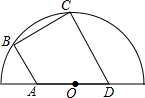 如图,四边形ABCD内接于半圆O,其中点A,D在直径上,点B,C在半圆弧上,AB∥CD,∠B=90°,若AO=3,∠BAD=120°,则BC=3$\sqrt{3}$.
如图,四边形ABCD内接于半圆O,其中点A,D在直径上,点B,C在半圆弧上,AB∥CD,∠B=90°,若AO=3,∠BAD=120°,则BC=3$\sqrt{3}$.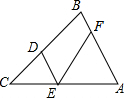 如图,在△ABC中,∠B=70°,点D,E,F分别在BC,AC,AB上,且CD=CE,AF=AE,则∠DEF=55°.
如图,在△ABC中,∠B=70°,点D,E,F分别在BC,AC,AB上,且CD=CE,AF=AE,则∠DEF=55°.