题目内容
10.先阅读第(1)题的解法,再解答第(2)题.(1)已知a,b是有理数,a≠0,并且满足5-$\sqrt{3}$a=2b+$\frac{2}{3}$$\sqrt{3}$-a,求a,b的值.
解:∵5-$\sqrt{3}$a=2b+$\frac{2}{3}$$\sqrt{3}$-a
∴5-$\sqrt{3}$a=(2b-a)+$\frac{2}{3}$$\sqrt{3}$
∴$\left\{\begin{array}{l}{2b-a=5}\\{-a=\frac{2}{3}}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{13}{6}}\end{array}\right.$
(2)已知x,y是有理数,并且满足等式x2-2y-$\sqrt{2}$y=26-5$\sqrt{2}$,求x+y的值.
分析 (1)已知等式整理后,利用等式性质求出a与b的值即可;
(2)仿照(1)的解题过程求出x与y的值,即可求出x+y的值.
解答 解:(1)∵5-$\sqrt{3}$a=2b+$\frac{2}{3}$$\sqrt{3}$-a,
∴5-$\sqrt{3}$a=(2b-a)+$\frac{2}{3}$$\sqrt{3}$,
∴$\left\{\begin{array}{l}{2b-a=5}\\{-a=\frac{2}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{13}{6}}\end{array}\right.$;
(2)∵x,y是有理数,并且满足等式x2-2y-$\sqrt{2}$y=26-5$\sqrt{2}$,
∴$\left\{\begin{array}{l}{{x}^{2}-2y=26}\\{y=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=±6}\\{y=5}\end{array}\right.$,
当x=6,y=5时,x+y=11;当x=-6,y=5时,x+y=-1.
点评 此题考查了解二元一次方程组,弄清题中的解题方法是解本题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
19.下列成语所描述的事件概率为0的是( )
| A. | 水中捞月 | B. | 守株待兔 | C. | 瓮中捉鳖 | D. | 十拿九稳 |
 在直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,6)
在直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,6) (尺规作图)如图,已知△ABC,请你在平面内找一点D,使得以A,B,C,D为顶点的四边形为平行四边形(画出一种情况即可).
(尺规作图)如图,已知△ABC,请你在平面内找一点D,使得以A,B,C,D为顶点的四边形为平行四边形(画出一种情况即可).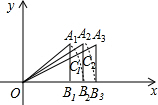 如图,在平面直角坐标系中,已知A1(1,1),B1(1,0),以O为圆心OA1为半径作圆弧交x轴于B2,作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1,以O为圆心OA2为半径作圆弧交x轴于B3,作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2,…,按此规律,则Cn的纵坐标为($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)(结果用n的代数式表示)
如图,在平面直角坐标系中,已知A1(1,1),B1(1,0),以O为圆心OA1为半径作圆弧交x轴于B2,作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1,以O为圆心OA2为半径作圆弧交x轴于B3,作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2,…,按此规律,则Cn的纵坐标为($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)(结果用n的代数式表示) 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=2,BC=3,如果边AB上的点P,使得以P,A,D为顶点的三角形与P,B,C为顶点的三角形相似,这样的点P有3个.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=2,BC=3,如果边AB上的点P,使得以P,A,D为顶点的三角形与P,B,C为顶点的三角形相似,这样的点P有3个.