题目内容
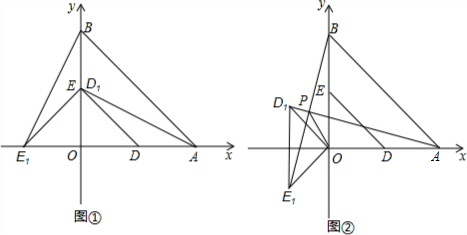
20.已知,在平面直角坐标系中,A(4,0),B(0,4),点D、E分别为OA、OB的中点,将△ODE绕点O逆时针旋转一定角度,得到△OD1E1,设旋转角为α,记直线AD1与BE1的交点为P.(Ⅰ)如图①,α=90°,则点D1的坐标是(0,2),线段AD1的长等于2$\sqrt{5}$;点E1的坐标是(-2,0),线段BE1的长等于2$\sqrt{5}$;
(Ⅱ)如图②,α=135°.
①求∠APO的大小;
②求$\frac{P{D}_{1}}{PB}$的值(直接写出结果即可)
分析 (1)由旋转的性质可知OD1=OD=2,OE1=OE=2,再由勾股定理即可求出AD1和BE1的长度;
(2)①先证∠APB=90°,则△AOB和△APB是有公共斜边的直角三角形,根据共斜边的两个直角三角形,则四个顶点共圆,得A、O、P、B四点共圆,从而得出结论;
②证△OD1P∽△AD1O,得$\frac{OP}{AO}=\frac{{D}_{1}P}{{D}_{1}O}$,则OP=2D1P,再证明△AOD1∽△BPO,得$\frac{AO}{BP}=\frac{O{D}_{1}}{PO}$,则BP=2PO,所以$\frac{P{D}_{1}}{PB}$=$\frac{1}{4}$.
解答 解:(1)如图1,∵点D、E分别是OA、OB的中点,
∴OE=2,OD=2,
由旋转的性质可知:OD1=OD=2,OE1=OE=2,
∴D1(0,2)、E1(-2,0),
∴由勾股定理可知:AD1=2$\sqrt{5}$,BE1=2$\sqrt{5}$,
故答案为:(0,2),2$\sqrt{5}$,(-2,0),2$\sqrt{5}$;
(2)①由旋转的性质可知:∠E1OB=∠D1OA,
在△E1OB与△D1OA中,
$\left\{\begin{array}{l}{O{E}_{1}=O{D}_{1}}\\{∠{E}_{1}OB=∠{D}_{1}OA}\\{OB=OA}\end{array}\right.$,
∴△E1OB≌△D1OA(SAS),
∴∠BE1O=∠AD1O,
又∵∠PCD1=∠OCE1,
∴∠D1PE1=∠D1OE1=90°,
∴∠AOB=∠APB=90°,
∴A、O、P、B四点共圆,
∴∠APO=∠OBA=45°;
②如图②,∵∠APO=45°,
∴∠D1PO=180°-45°=135°,
∵∠AOD1=135°,
∴∠AOD1=∠D1PO,
∵∠OD1A=∠OD1A,
∴△OD1P∽△AD1O,
∴$\frac{OP}{AO}=\frac{{D}_{1}P}{{D}_{1}O}$,
∵AO=4,D1O=2,
∴$\frac{OP}{4}=\frac{{D}_{1}P}{2}$,
∴OP=2D1P,
∵△E1OB≌△D1OA,
∴∠OAD1=∠OBE1,
∵∠BPO=90°+45°=135°,
∴∠BPO=∠AOD1,
∴△AOD1∽△BPO,
∴$\frac{AO}{BP}=\frac{O{D}_{1}}{PO}$,
∴BP=2PO,
∴BP=4PD1,
∴$\frac{P{D}_{1}}{PB}$=$\frac{1}{4}$.
点评 本题是几何变换的综合题,考查了等腰直角三角形、全等三角形及相似三角形的性质和判定,并通过证明四点共圆求出角的度数,本题的关键是证明三角形相似,通过相似对应边的比得出线段的倍数关系,从而得出最后的结论.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案 如图,直线y=mx(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A,B两点,过点A作AM垂直x轴,垂足为点M,连接BM,若S△AMB=3,则k的值为( )
如图,直线y=mx(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A,B两点,过点A作AM垂直x轴,垂足为点M,连接BM,若S△AMB=3,则k的值为( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
| A. | 一个平角就是一条直线 | |
| B. | 连接两点间的线段,叫做这两点的距离 | |
| C. | 两条射线组成的图形叫做角 | |
| D. | 经过两点有一条直线,并且只有一条直线 |
 有5个边长为1的正方形,排列形式如图:请把它们分割后拼接成一个大正方形.
有5个边长为1的正方形,排列形式如图:请把它们分割后拼接成一个大正方形. 在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题:
在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题: 如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积.
如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积. 如图,已知直线l:y=$\frac{5}{12}$x+$\frac{5}{4}$,点A,B的坐标分别是(1,0)和(6,0),点C在直线l上,当△ABC是直角三角形时,点C的坐标为(1,$\frac{5}{3}$)或(6,$\frac{15}{4}$)或($\frac{33}{13}$,$\frac{30}{13}$).
如图,已知直线l:y=$\frac{5}{12}$x+$\frac{5}{4}$,点A,B的坐标分别是(1,0)和(6,0),点C在直线l上,当△ABC是直角三角形时,点C的坐标为(1,$\frac{5}{3}$)或(6,$\frac{15}{4}$)或($\frac{33}{13}$,$\frac{30}{13}$).