题目内容
7.菱形的边长为5,一内角为60°,则较长对角线长为( )| A. | $\frac{5}{2}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 5 | D. | 5$\sqrt{3}$ |
分析 因为菱形的四条边都相等,所以AB=AD,又因为∠BAD=60°,所以△ABD为等边三角形,所以BD=5.又因为AC⊥BD,OA=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD=$\frac{5}{2}$,所以可求得OA的长,即可求得AC的长.
解答 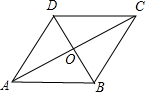 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,AD=AB=5,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=5,
∴OD=$\frac{5}{2}$,
∴OA=$\sqrt{3}$OD=$\frac{5\sqrt{3}}{2}$,
∴AC=5$\sqrt{3}$.
∴较长的对角线的长为5$\sqrt{3}$.
故选D.
点评 此题考查了菱形的性质、勾股定理等 知识,解题的关键是记住菱形的对角线互相平分且垂直,菱形的四条边都相等,学会用勾股定理求线段的长.

练习册系列答案
相关题目
18.2015年9月25日武汉园博园正式开园,其中在9月30日的游客人数为3.9万人.在接下来的国庆节七天假期中,每天的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)10月2日的人数为7.78万人
(2)国庆节七天假期里,游客人数最多的是10月3日,达到7.98万人;游客人数最少的是10月7日,达到3.08万人
(3)请问园博园在国庆节这七天内一共接待了多少游客?(结果精确到万位)
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (万人) | +2.1 | +1.78 | +0.2 | -0.8 | -1 | -1.6 | -1.5 |
(2)国庆节七天假期里,游客人数最多的是10月3日,达到7.98万人;游客人数最少的是10月7日,达到3.08万人
(3)请问园博园在国庆节这七天内一共接待了多少游客?(结果精确到万位)
17.下列算式正确的是( )
| A. | -1-1=0 | B. | 2-2÷(-$\frac{1}{3}$)=0 | C. | |5-2|=-(5-2) | D. | -23=-8 |

 如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于$\frac{1}{2}$AB长为半径作弧,两弧交于点C.若点C的坐标为(m-1,2n),则m与n的关系为m-1=2n.
如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于$\frac{1}{2}$AB长为半径作弧,两弧交于点C.若点C的坐标为(m-1,2n),则m与n的关系为m-1=2n.