Question

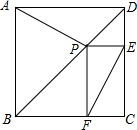已知：P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，E、F分别为垂足，
（1）求证：AP=EF．
（2）若∠BAP=60°，PD=

2

，求EF的长．

Answer 1

考点：正方形的性质,全等三角形的判定与性质,矩形的判定与性质

专题：

分析：（1）连接CP，证四边形EPFC是矩形，求出EF=PC，证△ABP≌△CBP，推出AP=CP即可；
（2）先根据△ABP≌△CBP得出∠BAP=∠BCP=60°，∠PCE=30°，再证△PFB是等腰直角三角形，求出PE的长度，再根据直角三角形的性质即可得出结论．

解答：（1）证明：连接PC，
∵ABCD是正方形，
∴∠C=90°，
∵PE⊥CD，PF⊥BC，
∴四边形PFCE是矩形，
∴EF=PC，
在△ABP和△CBP中，

AB=BC ∠ABP=∠CBP BP=BP

，
∴△ABP≌△CBP（SAS），
∴AP=CP，
∵EF=CP，
∴AP=EF．
（2）证明：∵由（1）知△ABP≌△CBP，
∴∠BAP=∠BCP=60°，
∴∠PCE=30°，
∵四边形ABCD是正方形，BD是对角线，
∴∠PDE=45°，
∵PE⊥CD，
∴DE=PE，
∵PD=

2

，
∴PE=1，
∴PC=2PE=2，
∵由（1）知EF=PC，
∴EF=2．

点评：本题考查的是正方形的性质，涉及到勾股定理，全等三角形的性质和判定等知识点的连接和掌握，能证出AP=PC是解此题的关键．