题目内容
△ABC中,∠A=a,
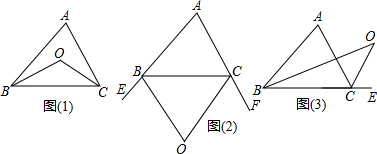
(1)若∠ABC,∠ACB的平分线相交于O,如图(1),求∠BOC的度数;
(2)若∠ABC,∠ACB的外角平分线相交于O,如图(2),求∠BOC的度数;
(3)若∠ABC的平分线与∠ACB的外角平分线相交于O,如图(3),求∠BOC的度数.

(1)若∠ABC,∠ACB的平分线相交于O,如图(1),求∠BOC的度数;
(2)若∠ABC,∠ACB的外角平分线相交于O,如图(2),求∠BOC的度数;
(3)若∠ABC的平分线与∠ACB的外角平分线相交于O,如图(3),求∠BOC的度数.
考点:三角形内角和定理,三角形的角平分线、中线和高,三角形的外角性质
专题:
分析:(1)根据∠A的度数,表示出另外两角的和,然后求出它们和的一半,利用三角形内角和定理求得即可;
(2)根据三角形外角的性质和角平分线的性质表示出两个角的和,求出它们的一半,利用三角形内角和定理表示出来即可;
(3)根据三角形外角的性质和角平分线的性质表示出两角和的一半,用180°减去两角和的一半即可.
(2)根据三角形外角的性质和角平分线的性质表示出两个角的和,求出它们的一半,利用三角形内角和定理表示出来即可;
(3)根据三角形外角的性质和角平分线的性质表示出两角和的一半,用180°减去两角和的一半即可.
解答:解:(1)∵∠A=a,
∴∠B+∠C=180°-a=180°-a,
∵OB、OC分别是∠ABC,∠ACB的平分线,
∴∠OBC+∠OCB=
(∠B+∠C)=
(180°-a)
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
(180°-a)=90°+
a;
(2)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A
=180°+a,
∵OB,OC分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠OBC+∠OCB=
(∠DBC+∠ECB)=
(180°+a),
∴∠O=180°-(∠OBC+∠OCB)=90°-
a;
(3)∵∠ACE=∠A+∠ABC且BO,CO分别是△ABC内角∠ABC与外角∠ACE的角平分线,
∴∠OCB+∠OBC=
∠ABC+∠ACB+
∠ACE=180°-
a,
∴∠O=180°-(∠OCB+∠OBC)
=180°-(180°-
a)
=
a.
∴∠B+∠C=180°-a=180°-a,
∵OB、OC分别是∠ABC,∠ACB的平分线,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A
=180°+a,
∵OB,OC分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠O=180°-(∠OBC+∠OCB)=90°-
| 1 |
| 2 |
(3)∵∠ACE=∠A+∠ABC且BO,CO分别是△ABC内角∠ABC与外角∠ACE的角平分线,
∴∠OCB+∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠O=180°-(∠OCB+∠OBC)
=180°-(180°-
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
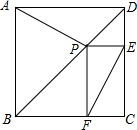 已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足,
已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足, 如图,你的同桌画了一个四边形ABCD,让你帮他检查四边形 ABCD是否为矩形,但你只能用一把带有刻度的直尺,请你设计一种方案,帮助同桌检测这个四边形是否为矩形.
如图,你的同桌画了一个四边形ABCD,让你帮他检查四边形 ABCD是否为矩形,但你只能用一把带有刻度的直尺,请你设计一种方案,帮助同桌检测这个四边形是否为矩形. 如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=2∠AOB,若AC=18cm,试求:
如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=2∠AOB,若AC=18cm,试求: 如图直角三角形中,三个正方形的边长分别为a,b,c,请证明:b=a+c.
如图直角三角形中,三个正方形的边长分别为a,b,c,请证明:b=a+c.