Question

16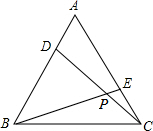．如图，D、E分别是等边三角形ABC的两边AB、AC上的点，且AD=CE，BE，DC相交于点P，则∠BPD的度数为60°．

Answer 1

分析 根据SAS证出△CAD≌△BCE，得出∠DCA=∠EBC，再根据∠BCD+∠DCA=60°，得出∠BPC=120°，再根据平角的定义即可得出∠BPD的度数．

解答 解：∵ABC是等边三角形，
∴∠BAC=∠ACB，AC=BC，
在△CAD和△BCE中，
$\left\{\begin{array}{l}{AD=CE}\\{∠BAC=∠ACB}\\{AC=BC}\end{array}\right.$，
∴△CAD≌△BCE（SAS），
∴∠DCA=∠EBC，
∵∠BCD+∠DCA=60°，
∴∠BPC=120°，
∴∠BPD=60°；
故答案为：60°．

点评 此题考查了三角形的判定与性质和等腰三角形的性质，根据全等证出∠DCA=∠EBC，得出∠BPC=120°是解决本题的关键．