题目内容
14.如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形;
(3)请利用备用图分析,在(2)的条件下,若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,求PF+PM的最小值,并求出此时线段BP的长.
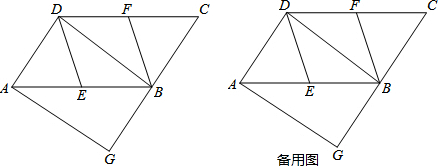
分析 (1)根据平行四边形的性质得到DF=BE,AB∥CD,根据平行四边形的判定定理证明四边形DEBF是平行四边形,根据平行四边形的性质证明结论;
(2)根据矩形的判定定理得到四边形AGBD是矩形,根据直角三角形的性质得到ED=EB,证明结论;
(3)连接EM交BD于P,根据轴对称的性质证明此时PF+PM的值最小,根据等边三角形的性质计算即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、CD的中点,
∴DF=BE,又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)∵AG∥DB,AD∥CG,
∴四边形AGBD是平行四边形,
∵∠G=90°,
∴平行四边形AGBD是矩形,
∴∠ADB=90°,又E为边AB的中点,
∴ED=EB,又四边形DEBF是平行四边形,
∴四边形DEBF是菱形;
(3)连接EF,连接EM交BD于P,
∵四边形DEBF是菱形,
∴点E和点F关于BD轴对称,此时PF+PM的值最小,
∵四边形DEBF是菱形,∠DEB=120°,
∴∠EBF=60°,
∴△BEF是等边三角形,又BE=4,
∴EM=2$\sqrt{3}$,即PF+PM的最小值为2$\sqrt{3}$,
由题意得,点P为△EBF的重心,
∴BP=$\frac{4\sqrt{3}}{3}$.
点评 本题考查的是平行四边形的判定和性质、菱形的判定和性质,轴对称变换的性质以及等边三角形的性质的综合运用,掌握相关的判定定理和性质定理、正确作出辅助性是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.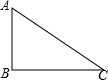 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
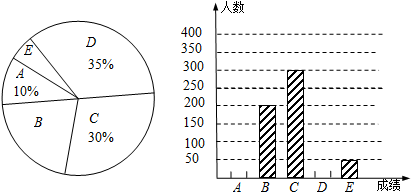
3.下列调查中,最适合采用抽样调查的是( )
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
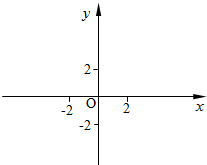 已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.
已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4. 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).