题目内容
13.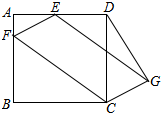 如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.
如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.
分析 过G作GH⊥CD于H,由四边形EFCG是平行四边形,得到EF∥CG,由正方形的性质得到AB∥CD,推出∠EFC+∠FCD+∠DCG=∠AFE+∠EFC+∠FCD=180°,然后通过三角形全等证得AE=HG=2,CH=AF=1,从而得到结果.
解答 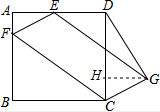 解;过G作GH⊥CD于H,
解;过G作GH⊥CD于H,
∵四边形EFCG是平行四边形,
∴EF∥CG,∵AB∥CD,
∴∠EFC+∠FCD+∠DCG=∠AFE+∠EFC+∠FCD=180°,
∴∠AFE=∠HCG,
在△AEF与△CHG中,
$\left\{\begin{array}{l}{∠A=∠GHC=90°}\\{∠AFE=∠HCG}\\{EF=CG}\end{array}\right.$,
∴△AEF≌△CHG,
∴AE=HG=2,CH=AF=1,
∴DH=3,
∴DG=$\sqrt{{3}^{3}{+2}^{2}}$=$\sqrt{13}$.
点评 本题考查了正方形的性质,平行四边形的性质,全等三角形的判定与性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.分解因式a2-9a的结果是( )
| A. | a(a-9) | B. | (a-3)(a+3) | C. | (a-3a)(a+3a) | D. | (a-3)2 |
5.四个实数:-1,-$\sqrt{2}$,0,1中,最小的实数是( )
| A. | -1 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
2.我们知道,每年的4月23日是”世界读书日”,某校为了鼓励学生去发现读书的乐趣,享受阅读的过程,随机调查了部分学生,就”你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表.请根据统计表提供的信息解答下列问题:
(1)这次随机调查了200名学生,统计表中d=0.13.
(2)假如以此统计表绘制出扇形统计图,则武侠小说对应的圆心角度数是多少?
| 各类 | 频数 | 频率 |
| 卡通画 | a | 0.56 |
| 时文杂志 | 32 | b |
| 武侠小说 | 30 | 0.15 |
| 文学名著 | c | d |
(2)假如以此统计表绘制出扇形统计图,则武侠小说对应的圆心角度数是多少?
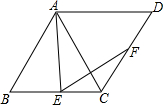 如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.
如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.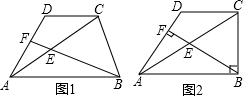 如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.
如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.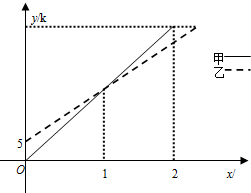 在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.两人在出发时都配备了通话距离为3km的对讲机,便于两人在骑车过程中可以用对讲机通话.下列说法:
在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.两人在出发时都配备了通话距离为3km的对讲机,便于两人在骑车过程中可以用对讲机通话.下列说法: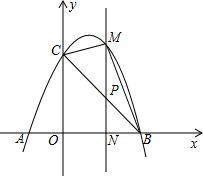 如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.