题目内容
用棋子按如图方式摆放，照此规律，第n个图形比第（n-1）个图形多 枚棋子．
考点：规律型：图形的变化类
专题：
分析：仔细观察图形，发现图形个数与棋子个数的关系式，然后得到通项公式，从而即可求解．
解答：解：观察图形得：
第1个图形有22=3个棋子；
第2个图形有32=9个棋子；
第3个图形有42=16个棋子；
…
第n-1个图形有（n-1）2个棋子；
第n个图形有n2个棋子；
所以：n个图形比第（n-1）个图形多n2-（n-1）2=（2n-1）个枚棋子，
故答案为：2n-1．
第1个图形有22=3个棋子；
第2个图形有32=9个棋子；
第3个图形有42=16个棋子；
…
第n-1个图形有（n-1）2个棋子；
第n个图形有n2个棋子；
所以：n个图形比第（n-1）个图形多n2-（n-1）2=（2n-1）个枚棋子，
故答案为：2n-1．
点评：本题考查了图形的变化类问题，解题的关键是找出数字之间的运算规律，利用规律解决问题．
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c的图象如图所示，下列判断中不正确的是（ ）| A、abc＜0 |
| B、b2-4ac＞0 |
| C、2a+b＞0 |
| D、4a-2b+c＜0 |
如果两个圆心角相等，那么（ ）
| A、这两个圆心角所对的弦相等 |
| B、这两个圆心角所对的弧相等 |
| C、这两个圆心角所对的弦的弦心距相等 |
| D、以上说法都不对 |
如图，已知正比例函数y=2x和反比例函数的图象交于点 A（m，-2）．
如图，如果在阳光下你的身影的方向为北偏西60°方向，那么太阳相对于你的方向是（ ）| A、南偏东60° |
| B、南偏东30° |
| C、南偏西60° |
| D、南偏西30° |
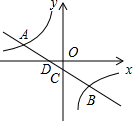如图，一次函数y=kx+b的图象与反比例函数