题目内容
16.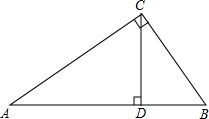 如图,在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4.
如图,在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4.
分析 根据图形可得△BDC∽△CDA,从而利用对应边成比例可得出CD的长度.
解答 解:∵∠BCD+∠ACD=90°,∠CAD+∠ACD=90°,
∴∠CAD=∠BCD,
∴△BDC∽△CDA,
故可得:$\frac{CD}{AD}=\frac{BD}{CD}$,即CD2=AD•BD=16,
∴CD=4.
故答案为:4.
点评 本题考查了相似三角形的判定和性质,解题的关键是熟记各种判定方法以及相似三角形的各种性质.

练习册系列答案
相关题目
1.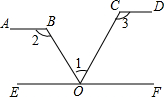 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=90° | C. | ∠1+∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
8.下列计算不正确的是( )
| A. | (-2)-2=-$\frac{1}{4}$ | B. | ($\frac{1}{3}$)-2=9 | ||
| C. | 20050=20080 | D. | 3.2×10-4=0.00032. |
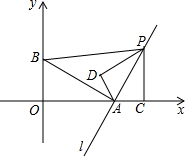 如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).