题目内容
1.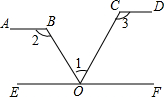 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=90° | C. | ∠1+∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
分析 由平行线的性质可用∠2、∠3分别表示出∠BOE和∠COF,再由平角的定义可找到关系式.
解答 解:
∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°-∠2,同理可得∠COF=180°-∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°-∠2+∠1+180°-∠3=180°,
即∠2+∠3-∠1=180°,
故选D.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
12.计算(ab2)•(-2a2b)2的结果是( )
| A. | 4a5b4 | B. | 2a5b4 | C. | 4a3b4 | D. | 4a5b5 |
6.下列各组数中,是二元一次方程3x-y=5的解的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
10.函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
| A. | k<3 | B. | k<3且k≠0 | C. | k≤3且k≠0 | D. | k≤3 |
11.下列计算中,正确的是( )
| A. | 2a+3b=5ab | B. | (3a3)2=6a6 | C. | a6+a2=a3 | D. | -3a+2a=-a |
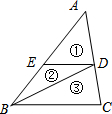 如图,DE∥BC,连接BD,△ABC被分成①②③三部分,其中图形①和②的面积相等,则图形②和③的面积比为1:2.
如图,DE∥BC,连接BD,△ABC被分成①②③三部分,其中图形①和②的面积相等,则图形②和③的面积比为1:2.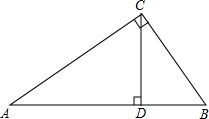 如图,在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4.
如图,在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4.