题目内容
7.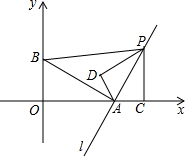 如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
分析 求出直线L的解析式,证出△AOB∽△PCA,得出$\frac{BO}{AO}$=$\frac{AC}{PC}$=$\frac{1}{2}$,设AC=m,则PC=2m,根据△PCA≌△PDA,得出$\frac{AD}{PD}$=$\frac{AC}{PC}$=$\frac{1}{2}$,当△PAD∽△PBA时,根据$\frac{AD}{PD}$=$\frac{BA}{PA}$=$\frac{1}{2}$,AB=2$\sqrt{5}$,求出AP=4$\sqrt{5}$,m2+(2m)2=(4$\sqrt{5}$)2,得出m=±4,从而求出P点的坐标为(8,8)、(0,-8),若△PAD∽△BPA,得出$\frac{PA}{BA}$=$\frac{AD}{PD}$=$\frac{1}{2}$,求出PA=$\sqrt{5}$,从而得出m2+(2m)2=($\sqrt{5}$)2,求出m=±1,即可得出P点的坐标为(5,2)、(3,-2).
解答 解:∵直线l过点A(4,0),且l⊥AB,
∴直线L的解析式为;y=2x-8,
∠BAO+∠PAC=90°,
∵PC⊥x轴,
∴∠PAC+∠APC=90°,
∴∠BAO=∠APC,
∵∠AOB=∠ACP,
∴△AOB∽△PCA,
∴$\frac{BO}{CA}$=$\frac{AO}{PC}$,
∴$\frac{BO}{AO}$=$\frac{AC}{PC}$=$\frac{1}{2}$,
设AC=m,则PC=2m,
∵△PCA≌△PDA,
∴AC=AD,PC=PD,
∴$\frac{AD}{PD}$=$\frac{AC}{PC}$=$\frac{1}{2}$,
如图1:当△PAD∽△PBA时,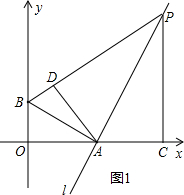
则$\frac{AD}{BA}$=$\frac{PD}{PA}$,
则$\frac{AD}{PD}$=$\frac{BA}{PA}$=$\frac{1}{2}$,
∵AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴AP=4$\sqrt{5}$,
∴m2+(2m)2=(4$\sqrt{5}$)2,
∴m=±4,
当m=4时,PC=8,OC=8,P点的坐标为(8,8),
当m=-4时,如图2,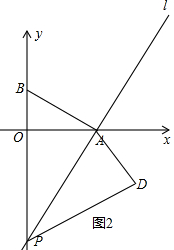
PC=8,OC=0,P点的坐标为(0,-8),
如图3,若△PAD∽△BPA,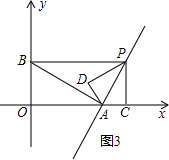
则$\frac{PA}{BA}$=$\frac{AD}{PD}$=$\frac{1}{2}$,
PA=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$,
则m2+(2m)2=($\sqrt{5}$)2,
∴m=±1,
当m=1时,PC=2,OC=5,P点的坐标为(5,2),
当m=-1时,如图4,PC=2,OC=3,P点的坐标为(3,-2);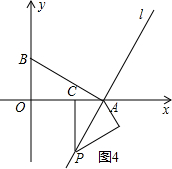
则所有满足此条件的点P的坐标是:P(5,2 ),p(8,8),P(0,-8),P(3,-2).
故答案为:P(5,2 ),p(8,8),P(0,-8),P(3,-2).
点评 此题考查了一次函数的综合,用到的知识点是相似三角形和全等三角形的判定与性质、勾股定理、一次函数等,关键是根据题意画出图形,注意有四个点.

| A. | 4a5b4 | B. | 2a5b4 | C. | 4a3b4 | D. | 4a5b5 |
| A. | $±\sqrt{0.25}$=±0.5 | B. | $±\sqrt{0.25}$=0.5 | ||
| C. | 0.5是0.25的平方根 | D. | 0的平方根是0 |
| A. | ⊙O1 | B. | ⊙O2 | ||
| C. | 两圆增加的面积是相同的 | D. | 无法确定 |
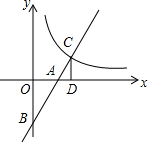 如图,直线y=kx-2(k>0)与双曲线$y=\frac{k}{x}$在第一象限内的交点为C,与x轴,y轴的交点分别为A,B,过点C作CD⊥x轴,垂足为D.若△OAB与△ACD的面积比为4:1,则k的值等于$\sqrt{3}$.
如图,直线y=kx-2(k>0)与双曲线$y=\frac{k}{x}$在第一象限内的交点为C,与x轴,y轴的交点分别为A,B,过点C作CD⊥x轴,垂足为D.若△OAB与△ACD的面积比为4:1,则k的值等于$\sqrt{3}$.
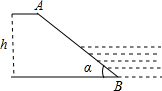 如图所示,一水库迎水坡AB的坡度i=1:2,则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$.
如图所示,一水库迎水坡AB的坡度i=1:2,则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$.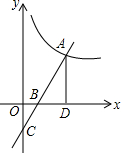 如图,直线y=2x-4与反比例函数y=$\frac{k}{x}$的图象交于第一象限的点A,与x轴、y轴分别交于点B,C,AD⊥x轴于点D.如果△BOC与△BDA的面积之比等于4:9,则k=30.
如图,直线y=2x-4与反比例函数y=$\frac{k}{x}$的图象交于第一象限的点A,与x轴、y轴分别交于点B,C,AD⊥x轴于点D.如果△BOC与△BDA的面积之比等于4:9,则k=30.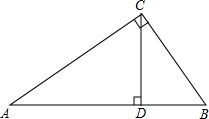 如图,在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4.
如图,在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4.