题目内容
6. 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$(1)已知点A(0,1),B(4,1),C(3,-1),D(3,-2),连接AB,CD.
①对于线段AB和线段CD,若点A和C被点P“关联”,则点P的坐标为($\frac{3}{2}$,0);
②线段AB和线段CD的一“中位点”是Q (2,-$\frac{1}{2}$),求这两条线段上被点Q“关联”的两个点的坐标;
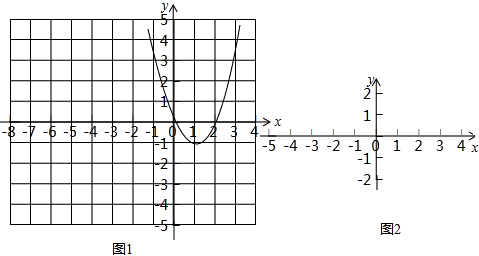
(2)如图1,已知点R(-2,0)和抛物线W1:y=x2-2x,对于抛物线W1上的每一个点M,在抛物线W2上都存在点N,使得点N和M 被点R“关联”,请在图1 中画出符合条件的抛物线W2;
(3)正方形EFGH的顶点分别是E(-4,1),F(-4,-1),G(-2,-1),H(-2,1),⊙T的圆心为T(3,0),半径为1.请在图2中画出由正方形EFGH和⊙T的所有“中位点”组成的图形(若涉及平面中某个区域时可以用阴影表示),并直接写出该图形的面积.
分析 (1)①点M 和N被点P“关联”的定义即可解决问题.
②设在线段AB和线段CD上分别存在K(x,1)和L(3,y)被点Q(2,-$\frac{1}{2}$)“关联”,则点Q是KL中点,列出方程即可解决问题.
(2)锐角题意可知画出抛物线W1关于点R的中心对称图形即可.
(3)先根据题意画出图形,再求出图形面积即可.
解答 解:(1)①∵点A和C被点P“关联”,
又∵$\frac{0+3}{2}$=$\frac{3}{2}$,$\frac{1-1}{2}$=0,
∴点P坐标($\frac{3}{2}$,0),
故答案为($\frac{3}{2}$,0).
②设在线段AB和线段CD上分别存在K(x,1)和L(3,y)被点Q(2,-$\frac{1}{2}$)“关联”,则点Q是KL中点,
∴2=$\frac{x+3}{2}$,-$\frac{1}{2}$=$\frac{1+y}{2}$,
∴x=1,y=-2,
∴这两条线段上被点Q“关联”的两个点的坐标分别是(1,1)和(3,-2).
(2)所求作的抛物线如图1所示,
(3)正方形EFGH和⊙T的所有“中位点”组成的图形如图2所示(影阴部分包括边界),
S阴=2×2-4[$\frac{1}{2}$×$\frac{1}{2}$-$\frac{1}{4}$•π•($\frac{1}{2}$)2]=3+$\frac{π}{4}$.
点评 本题考查二次函数综合题、中心对称等知识,解题的关键是理解题意,学会正确画出图形,利用分割法求面积,解题的难点是第三个问题的图不容易画出来,属于中考压轴题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
18.下列计算正确的是( )
| A. | 4x-3x=1 | B. | x2+x2=2x4 | C. | (x2)3=x6 | D. | 2x2•x3=2x6 |
18. 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m=6,n=20%;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | m | 3.41 | 90% | n |
| 八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(2)直接写出表中的m=6,n=20%;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
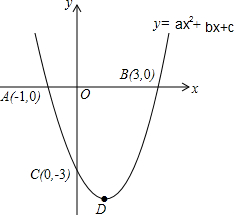 如图,抛物线y=ax2+bx+c的图象与x轴交于A(-1.0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D.
如图,抛物线y=ax2+bx+c的图象与x轴交于A(-1.0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D.



 阅读下列材料:
阅读下列材料: 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式. 如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:
如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中: