题目内容
20.图形与分析同样大小的小正方形纸片,按如图1的方式拼正方形.

第①个图形有1个小正方形纸片,第②个图形比第①个图形多3个小正方形纸片,第③个图形比第②个图形多5个小正方形纸片.
…
(1)第④个图形比第③个图形多7个小正方形纸片,小丽尝试从图形进行分析:
第一步:在图④中把多出的7个小正方形纸片分成几个部分,画上不同的斜线;
第二步:相应地,写出一个运算结果是7的算式.
请你写出小丽的分析过程.
(2)根据小丽的分析,第n+1个图形比第n个图形多多少个小正方形纸片?类比(1)写出相应的算式;
类比迁移
类似地,请在图Ⅱ中画出一组新的图形(4)个,使这组图形与图1中的图形具有相同的变化规律.
分析 (1)把7分成3部分,7=3+3+1=2×3+1,由此画出图形即可;
(2)根据已知图形得出第2个图形比第1个图形多:4-1=3个;第3个图形比第2个图形多:9-4=5个;第4个图形比第3个图形多:16-9=7个;即可得出后面一个图形比前面一个图形多的个数是连续奇数,进而得出公式第n个图形比第(n-1)个图形多2n-1个小正方形;由此利用规律得出答案即可.
解答 解:(1)如图,
3+3+1=2×3+1=7.
(2)第n个图形比第(n-1)个图形多2n-1个小正方形.
点评 此题主要考查了图形的变化规律,利用已知图形得出图形相邻之间的个数变化规律是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如图,图(1)是一个扇形AOB,将其作如下划分:第一次划分:如图(2)所示,得到扇形的总数为6个,分别为:扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB;第二次划分:如图(3)所示,在扇形C1OB1中,按上述划分方式继续划分,可以得到扇形的总数为11个;第三次划分:如图(4)所示;
依次划分下

(1)根据题意,完成表格
(2)请判断,按上述方式继续划分,能否得到扇形的总数为2000个?为什么?
依次划分下

(1)根据题意,完成表格
| 划分次数 | 扇形总个数 |
| 1 | 6 |
| 2 | 11 |
| 3 | 16 |
| 4 | 21 |
| … | … |
| n | 5n+1 |
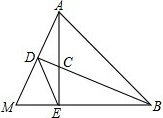 如图,AE、BD是△ABM的高,AE、BD交于点C,AE=BE,BD平分∠ABM.
如图,AE、BD是△ABM的高,AE、BD交于点C,AE=BE,BD平分∠ABM.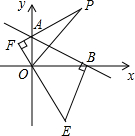 如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点
如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点 甲、乙两车同时以一定的速度从A城出发前往B城,行驶途中甲接到电话,立刻以同样的速度返回A城,然后提高速度前往B城,结果比乙车早到1小时,设甲、乙两车从A城出发的时间为t(小时),距离A城距离为y km,如图所示,则A,B两城距离是300km.
甲、乙两车同时以一定的速度从A城出发前往B城,行驶途中甲接到电话,立刻以同样的速度返回A城,然后提高速度前往B城,结果比乙车早到1小时,设甲、乙两车从A城出发的时间为t(小时),距离A城距离为y km,如图所示,则A,B两城距离是300km. 如图,在△ABC中,∠C=90°,正方形DEFG内接于△ABC,其中点D、E在边AB上,点F、G分别在边BC,CA上,已知$\frac{AC}{BC}$=k,则AD:DE:EB=k2:k:1(用k表示)
如图,在△ABC中,∠C=90°,正方形DEFG内接于△ABC,其中点D、E在边AB上,点F、G分别在边BC,CA上,已知$\frac{AC}{BC}$=k,则AD:DE:EB=k2:k:1(用k表示)