题目内容
18.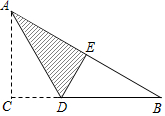 如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )| A. | x2=(8-x)2+62 | B. | x2=(8-x)2+42 | C. | x=8-x+4 | D. | x2=62+82 |
分析 由勾股定理求出AB=10,由折叠的性质得出DE=CD=8-x,AE=AC=6,∠AED=∠C=90°,得出BE=4,在Rt△BDE中,由勾股定理得出方程即可.
解答 解:∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵BD=x,
∴CD=8-x,
由折叠的性质得:DE=CD=8-x,AE=AC=6,∠AED=∠C=90°,
∴∠BED=90°,
∴BE=AB-AE=10-6=4,
在Rt△BDE中,由勾股定理得:BD2=DE2+BE2,
即x2=(8-x)2+42;
故选:B.
点评 本题考查了图形的折叠以及勾股定理的应用,正确利用勾股定理列方程是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.点P(2,-3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.某企业去年7月份产值为a万元,8月份比7月份减少了10%,9月份比8月份增加了15%,则9月份的产值是( )
| A. | (a-10%)(a+15%)万元 | B. | a(1-10%)(1+15%)万元 | C. | (a-10%+15%)万元 | D. | a(1-10%)(1+15%)万元 |
 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF. 如图,两圆圆心相同,大圆的弦AB与小圆相切,若图中阴影部分的面积是16π,则AB的长为8.
如图,两圆圆心相同,大圆的弦AB与小圆相切,若图中阴影部分的面积是16π,则AB的长为8.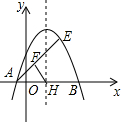 如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).