题目内容
12. 如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.
如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.
分析 设水塔的高AB为x米,根据直角三角形的性质、正确的定义分别求出BD、BC,根据题意列出方程,解方程即可.
解答 解:设水塔的高AB为x米,
∵∠ABD=45°,
∴BD=AB=x,
∴BC=20+x,
∵∠ACB=30°,
∴BC=$\frac{AB}{tan30°}$=$\sqrt{3}$x,
∴$\sqrt{3}$x=x+20,
解得,x=10$\sqrt{3}$+10,
答:水塔的高AB为(10$\sqrt{3}$+10)米.
点评 本题考查的是解直角三角形的应用、掌握仰角俯角的概念、锐角三角函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知一条圆弧所在圆的半径为24,所对的圆心角为60°,则这条弧长为( )
| A. | 4 | B. | 4π | C. | 8 | D. | 8π |
3.某企业去年7月份产值为a万元,8月份比7月份减少了10%,9月份比8月份增加了15%,则9月份的产值是( )
| A. | (a-10%)(a+15%)万元 | B. | a(1-10%)(1+15%)万元 | C. | (a-10%+15%)万元 | D. | a(1-10%)(1+15%)万元 |
10.若a,b,c均为非零实数,且a+b+c=abc=a3,则ab+bc+ca的最小值为( )
| A. | 6 | B. | 8 | C. | 9 | D. | 13 |
7. 如图,已知AC与BC相交于点O,∠C=∠D=75°,∠A=35°,则∠B的度数为( )
如图,已知AC与BC相交于点O,∠C=∠D=75°,∠A=35°,则∠B的度数为( )
 如图,已知AC与BC相交于点O,∠C=∠D=75°,∠A=35°,则∠B的度数为( )
如图,已知AC与BC相交于点O,∠C=∠D=75°,∠A=35°,则∠B的度数为( )| A. | 25° | B. | 35° | C. | 40° | D. | 45° |
8. 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )| A. | 12π-16$\sqrt{7}$ | B. | 16π-18$\sqrt{7}$ | C. | 16π-24$\sqrt{7}$ | D. | 16π-12$\sqrt{7}$ |
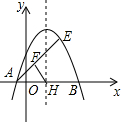 如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).