题目内容
14．
如图，四边形ABCD内接于⊙O，点E是BC延长线上一点，连接OB、OD，∠DCE=55°，则∠BOD=110°．
分析 首先根据邻补角的定义求得∠BCD的度数，然后利用圆内接四边形的性质求得∠A的度数，然后利用圆周角定理求得∠BOD的度数．
解答 解：∵∠DCE=55°，
∴∠BCD=125°，
∵四边形ABCD内接于⊙O，
∴∠A=55°，
∴∠BOD=2∠A=110°，
故答案为：110°．
点评 本题考查了圆内接四边形的性质，注意：①圆内接四边形的对角互补，②圆内接四边形的任意一个外角等于它的内对角．
练习册系列答案
相关题目
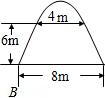如图，某学校的校门是一抛物线形状的建筑物，地面宽度为8m，两侧距地面6m高处各有一个挂校名横匾用的铁环，两铁环的水平距离为4m，则校门的高度为8m．
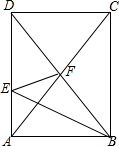如图，矩形ABCD的面积为36，BE平分∠ABD，交AD于E，沿BE将△ABE折叠，点A的对应点刚好落在矩形两条对角线的交点F处，则△ABE的面积为6．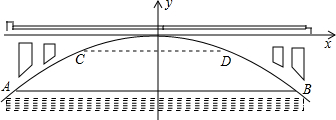
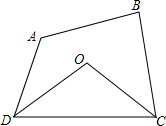如图，在四边形ABCD中，∠A+∠B=210°，且∠ADC与∠DCB的平分线相交于O，求∠COD的度数．