题目内容
AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=n°,求∠BED的度数(用含n的代数式表示).

(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=n°,求∠BED的度数(用含n的代数式表示).

考点:平行线的性质
专题:
分析:(1)根据角平分线的定义可得∠EDC=
∠ADC,然后代入数据计算即可得解;
(2)根据角平分线的定义表示出∠CBE,再根据两直线平行,内错角相等可得∠BCD=∠ABC,然后根据三角形的内角和定理列式整理即可;
(3)根据角平分线的定义求出∠ADE、∠ABE,根据两直线平行,同旁内角互补求出∠BAD,再根据四边形的内角和定理列式计算即可得解.
| 1 |
| 2 |
(2)根据角平分线的定义表示出∠CBE,再根据两直线平行,内错角相等可得∠BCD=∠ABC,然后根据三角形的内角和定理列式整理即可;
(3)根据角平分线的定义求出∠ADE、∠ABE,根据两直线平行,同旁内角互补求出∠BAD,再根据四边形的内角和定理列式计算即可得解.
解答:解:(1)∵DE平分∠ADC,ADC=70°,
∴∠EDC=
∠ADC=35°;
(2)∵BE平分∠ABC,
∴∠CBE=
∠ABC=
n°,
∵AB∥CD,
∴∠BCD=∠ABC=n°,
∴∠CBE+∠BED=∠EDC+∠ACD,
即
n°+∠BED=35°+n°,
解得∠BED=35°+
n°;
(3)如图,∵BE平分∠ABC,DE平分∠ADC,
∴∠ADE=
∠ADC=35°,∠ABE
∠ABC=
n°,
∵AB∥CD,
∴∠BAD=180°-∠ADC=180°-70°=110°,
在四边形ADEB中,∠BED=360°-110°-70°-
n°=215°-
n°.
∴∠EDC=
| 1 |
| 2 |
(2)∵BE平分∠ABC,
∴∠CBE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,

∴∠BCD=∠ABC=n°,
∴∠CBE+∠BED=∠EDC+∠ACD,
即
| 1 |
| 2 |
解得∠BED=35°+
| 1 |
| 2 |
(3)如图,∵BE平分∠ABC,DE平分∠ADC,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠BAD=180°-∠ADC=180°-70°=110°,
在四边形ADEB中,∠BED=360°-110°-70°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了平行线的性质,角平分线的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
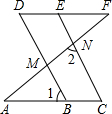 如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程:
如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程: