题目内容
19．下列说法正确的是（ ）| A． | 一个有理数的平方根有两个，它们互为相反数 | |
| B． | 负数没有立方根 | |
| C． | 无理数都是带根号的数 | |
| D． | 无理数都是无限小数 |
分析 根据实数的平方根的性质即可判定A；根据立方根的性质判定B选项；根据无理数的定义即可判定C、D选项．
解答 解：A．一个正数的平方根有两个，他们是互为相反数，故A选项错误；
B．负数没有平方根，但是负数有立方根，故B选项错误；
C．π是无理数，但是不带根号，故C选项的说法是错误的；
D．无理数都是无限不循环小数，故D选项是正确的．
故选：D．
点评 本题主要考查实数的相关的概念，熟记实数的相关的概念是解决此题的关键．
练习册系列答案
相关题目
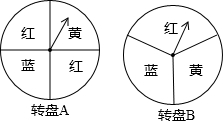小明和小芳做一个“配色”的游戏，下图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色，这种情况下小芳获胜；同样，蓝色和黄色在一起配成绿色，这种情况下小明获胜；在其它情况下，则小明、小芳不分胜负．
7．如果（x2+px+q）（x2+7）的展开式中不含x2与x3的项，那以p，q的值是（ ）
| A． | p=1，q=7 | B． | p=0，q=-7 | C． | p=2，q=1 | D． | p=0，q=7 |
4．在-22，-（-2），+（-$\frac{1}{2}$），-|-2|这四个数中，负数的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
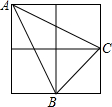如图，由四个边长为1的小正方形构成一个大正方形，连结小正方形的三个顶点，可得到△ABC，则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$．
8．下列说法正确的是（ ）
| A． | -5是25的平方根 | B． | 25的平方根是-5 | ||
| C． | $\sqrt{16}$是$\root{3}{-27}$的算术平方根 | D． | $\sqrt{3}$是$\sqrt{{{（-3）}^2}}$的算术平方根 |
9．一元二次方程（x-2）（x+3）=0根的情况是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 有一个实数根 | D． | 没有实数根 |