题目内容
14.解方程:(1)-x2+4x-3=0(用配方法解)
(2)3x(x-1)=2-2x(用适当的方法解)
分析 (1)首先两边同时除以-1,把二次项系数化为1,然后把-3移项,再两边同时加上4配方,然后两边直接开平方即可;
(2)首先把方程右边分解因式,然后移项可得3x(x-1)-2(1-x)=0,再提公因式x-1可得(x-1)(3x+2)=0,进而可得x-1=0,3x+2=0,再解即可.
解答 解:(1),-x2+4x-3=0,
x2-4x+3=0,
x2-4x=-3,
x2-4x+4=-3+4,
(x-2)2=1,
x-2=1,x-2=-1,
故x=1 或x=3;
(2)3x(x-1)=2-2x,
3x(x-1)=2(1-x),
3x(x-1)-2(1-x)=0,
(x-1)(3x+2)=0,
x-1=0,3x+2=0,
故x1=1,x2=-$\frac{2}{3}$.
点评 此题主要考查了因式分解法解一元二次方程,以及配方法解一元二次方程,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
9.下列是勾股数的是( )
| A. | 7,8,9 | B. | 5,7,12 | C. | 13,15,17 | D. | 21,28,35 |
19.下列说法正确的是( )
| A. | 一个有理数的平方根有两个,它们互为相反数 | |
| B. | 负数没有立方根 | |
| C. | 无理数都是带根号的数 | |
| D. | 无理数都是无限小数 |
6.已知m、n均为非零有理数,下列结论正确的是( )
| A. | 若m≠n,则|m|≠|n| | B. | 若|m|=|n|,则m=n | C. | 若m>n>0,则$\frac{1}{m}$>$\frac{1}{n}$ | D. | 若m>n>0,则m2>n2 |
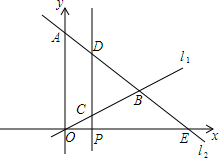 如图,在平面直角坐标系中,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).在x轴上有一点P(a,0),过点P作x轴的垂线分别交直线l1、l2于点C、D,直线l2与x轴交于点E.
如图,在平面直角坐标系中,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).在x轴上有一点P(a,0),过点P作x轴的垂线分别交直线l1、l2于点C、D,直线l2与x轴交于点E.