题目内容
13.(1)$\frac{-1}{x+1}$-$\frac{3x}{x+1}$(例题);解:原式=$\frac{-3-3x}{x+1}$
=$\frac{-3(x+1)}{x+1}$
=-3
(2)$\frac{a}{a+1}+\frac{1}{a+1}$;
(3)$\frac{a}{(a+1)^{2}}+\frac{1}{(a+1)^{2}}$;
(4)$\frac{5}{(x+1)^{2}}-\frac{5x}{(x-1)^{2}}$;
(5)$\frac{{a}^{2}}{a+b}+\frac{{b}^{2}+2ab}{a+b}$;
(6)$\frac{{a}^{2}-{c}^{2}}{a-b}+\frac{{b}^{2}-{c}^{2}}{b-a}$.
分析 原式各项变形后,利用同分母分式的加减法则计算即可得到结果.
解答 解:(2)原式=$\frac{a+1}{a+1}$=1;
(3)原式=$\frac{a+1}{(a+1)^{2}}$=$\frac{1}{a+1}$;
(4)原式=$\frac{5(x-1)^{2}-5x(x+1)^{2}}{(x+1)^{2}(x-1)^{2}}$;
(5)原式=$\frac{(a+b)^{2}}{a+b}$=a+b;
(6)原式=$\frac{{a}^{2}-{c}^{2}-{b}^{2}+{c}^{2}}{a-b}$=$\frac{(a+b)(a-b)}{a-b}$=a+b.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.检验下列各方程的解正确的是( )
| A. | 2x-1=$\frac{2}{3}-3x(x=\frac{1}{3})$ | B. | 1=$\frac{x}{2}-4$(x=-10) | ||
| C. | 4x+2=-x-3(x=1) | D. | 0.48x-6=0.02x(x=1.2) |
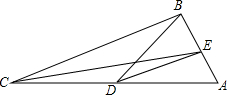 如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.
如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°. 如图,一个矩形广场的长为60m,宽为40m,广场内两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内外边缘所围成的两个矩形相似?
如图,一个矩形广场的长为60m,宽为40m,广场内两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内外边缘所围成的两个矩形相似?