题目内容
1．
如图，一个矩形广场的长为60m，宽为40m，广场内两条纵向小路的宽均为1.5m，如果设两条横向小路的宽都为x m，那么当x为多少时，小路内外边缘所围成的两个矩形相似？
分析 根据相似多边形的性质：对应边的比相等列出比例式，解出x的值即可．
解答 解：∵小路内外边缘所围成的两个矩形相似，
∴$\frac{60}{40}$=$\frac{60-3}{40-2x}$，
解得，x=1m，
答：当x为1m时，小路内外边缘所围成的两个矩形相似．
点评 本题考查的是相似多边形的性质，掌握相似多边形的性质：对应边的比相等是解题的关键．
练习册系列答案
相关题目
12．
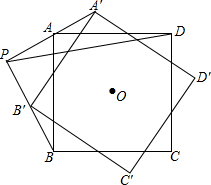如图，点O是正方形ABCD中的对称中心，AB=2，将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′，直线AA′与直线BB′交于点P，则线段PD长度的最大值为（ ）
如图，点O是正方形ABCD中的对称中心，AB=2，将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′，直线AA′与直线BB′交于点P，则线段PD长度的最大值为（ ）| A． | $\sqrt{5}$ | B． | 1 | C． | $\sqrt{5}$+1 | D． | $\sqrt{5}$-1 |